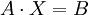Conjugate gradient methods
From CFD-Wiki
(Difference between revisions)
(added dot product) |
|||
| Line 2: | Line 2: | ||
For the system of equations: <br> | For the system of equations: <br> | ||
| - | :<math> | + | :<math> A \cdot X = B </math> <br> |
The unpreconditioned conjugate gradient method constructs the '''i'''th iterate <math>x^{(k)}</math> as an element of <math> x^{(k)} + span\left\{ {r^{(0)} ,...,A^{i - 1} r^{(0)} } \right\} </math> so that so that <math> \left( {x^{(0)} - \hat x} \right)^T A\left( {x^{(i)} - \hat x} \right) </math> is minimized , where <math> {\hat x} </math> is the exact solution of <math> AX = B </math>. <br> | The unpreconditioned conjugate gradient method constructs the '''i'''th iterate <math>x^{(k)}</math> as an element of <math> x^{(k)} + span\left\{ {r^{(0)} ,...,A^{i - 1} r^{(0)} } \right\} </math> so that so that <math> \left( {x^{(0)} - \hat x} \right)^T A\left( {x^{(i)} - \hat x} \right) </math> is minimized , where <math> {\hat x} </math> is the exact solution of <math> AX = B </math>. <br> | ||
Revision as of 20:34, 15 December 2005
Basic Concept
For the system of equations:
The unpreconditioned conjugate gradient method constructs the ith iterate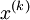 
as an element of 
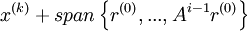so that so that 
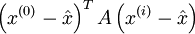is minimized , where 
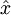is the exact solution of 
.
This minimum is guaranteed to exist in general only if A is symmetric positive definite. The preconditioned version of these methods use a different subspace for constructing the iterates, but it satisfies the same minimization property over different subspace. It requires that the preconditioner M is symmetric and positive definite.
Return to Numerical Methods
