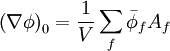Gradient computation
From CFD-Wiki
(Difference between revisions)
| Line 14: | Line 14: | ||
# Weighted interpolation: <math> \phi _f = w\phi _1 + \left( {1 - w} \right)\phi _0 </math> | # Weighted interpolation: <math> \phi _f = w\phi _1 + \left( {1 - w} \right)\phi _0 </math> | ||
#Arithmatic Average: <math> \phi _f = 0.5 \left( \phi _1 + \phi _0 \right) </math> | #Arithmatic Average: <math> \phi _f = 0.5 \left( \phi _1 + \phi _0 \right) </math> | ||
| + | |||
| + | == Note == | ||
| + | The above mentioned gradients are sometimes called '''unlimited gradients''' since the face value obtained from them can exceed the bounding cell values. For this reason, for implementing higher order schemes, it becomes important to restrict them, so as not to introduce over and undershoot of variables. | ||
Revision as of 03:02, 3 October 2005
Gradient Calculation
From Green-Gauss theorem:
Written in discrete form:
Value at Face
There are many ways of estimating value of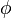 
at face.
- Weighted interpolation:
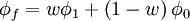
- Arithmatic Average:
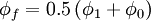
Note
The above mentioned gradients are sometimes called unlimited gradients since the face value obtained from them can exceed the bounding cell values. For this reason, for implementing higher order schemes, it becomes important to restrict them, so as not to introduce over and undershoot of variables.
