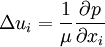Stokes flow
From CFD-Wiki
(Difference between revisions)
(There is no minus in the equation and the dynamic viscosity \mu is forgoten) |
|||
| Line 12: | Line 12: | ||
:<math> | :<math> | ||
| - | \Delta u_i = | + | \Delta u_i = \frac{1}{\mu} \frac{\partial p}{\partial x_i} |
</math> | </math> | ||
Latest revision as of 08:30, 20 August 2013
Stokes flow is the flow of a highly viscous fluid. Since a high viscosity coefficient implies a low Reynolds number, Stokes flow is also refered to as low Reynolds number flow or creeping flow.
Contents |
Governing equations
- Continuity equation
- Momentum equation