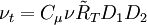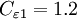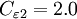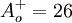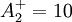Baldwin-Barth model
From CFD-Wiki
(Difference between revisions)
| Line 1: | Line 1: | ||
==Kinematic Eddy Viscosity== | ==Kinematic Eddy Viscosity== | ||
:<math> \nu _t = C_\mu \nu \tilde R_T D_1 D_2 </math> | :<math> \nu _t = C_\mu \nu \tilde R_T D_1 D_2 </math> | ||
| + | ==Turbulence Reynolds Number == | ||
| + | |||
| + | :<math> | ||
| + | {\partial \over {\partial t}}\left( {\nu \tilde R_T } \right) = U_j {\partial \over {\partial x_j }}\left( {\nu \tilde R_T } \right) = \left( {C_{\varepsilon 2} f_2 - C_{\varepsilon 1} } \right)\sqrt {\nu \tilde R_T P} + \left( {\nu + {{\nu _T } \over {\sigma _\varepsilon }}} \right){{\partial ^2 } \over {\partial x_k \partial x_k }} - {1 \over {\sigma _\varepsilon }}{{\partial \nu _T } \over {\partial x_k }}{{\partial \left( {\nu \tilde R_T } \right)} \over {\partial x_T }} | ||
| + | </math> | ||
| + | |||
| + | |||
| + | == Closure Coefficients and Auxilary Relations == | ||
| + | |||
| + | :<math> | ||
| + | C_{\varepsilon 1} = 1.2 | ||
| + | </math> <br> | ||
| + | :<math> | ||
| + | C_{\varepsilon 2} = 2.0 | ||
| + | </math> <br> | ||
| + | :<math> | ||
| + | C_\mu = 0.09 | ||
| + | </math> <br> | ||
| + | :<math> | ||
| + | A_o^ + = 26 | ||
| + | </math> <br> | ||
| + | :<math> | ||
| + | A_2^ + = 10 | ||
| + | </math> <br> | ||
Revision as of 08:59, 26 September 2005
Kinematic Eddy Viscosity
Turbulence Reynolds Number