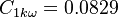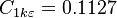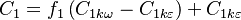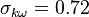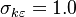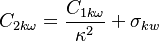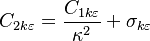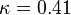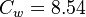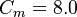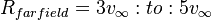CFD Online Logo CFD Online URL
www.cfd-online.com
[Sponsors]
Home > Wiki > Wray-Agarwal(WA) Turbulence Model

Wray-Agarwal(WA) Turbulence Model

From CFD-Wiki

(Difference between revisions)
Jump to: navigation, search
(→Introduction)
(→WA Model)
Line 2: Line 2:
The Wray-Agarwal (WA 2017m) model is a one-equation linear eddy viscosity model that was derived from two-equation <math>k-\omega</math> closure. It combines the most desirable characteristics of the one-equation <math>k-\epsilon</math> model and one-equation <math>k-\omega</math> model, analogous to the SST <math>k-\omega</math> model which combines best features of two-equation <math>k-\epsilon</math> and <math>k-\omega</math> models.
The Wray-Agarwal (WA 2017m) model is a one-equation linear eddy viscosity model that was derived from two-equation <math>k-\omega</math> closure. It combines the most desirable characteristics of the one-equation <math>k-\epsilon</math> model and one-equation <math>k-\omega</math> model, analogous to the SST <math>k-\omega</math> model which combines best features of two-equation <math>k-\epsilon</math> and <math>k-\omega</math> models.
-
==WA Model==
+
==WA Model (WA 2017m) ==
'''The turbulent eddy viscosity is given by:'''
'''The turbulent eddy viscosity is given by:'''
Line 88: Line 88:
C_{m} = 8.0
C_{m} = 8.0
</math>
</math>
-
 
==Boundary Conditions==
==Boundary Conditions==

Revision as of 21:16, 22 January 2021

Contents

Introduction

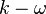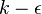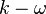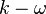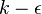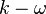The Wray-Agarwal (WA 2017m) model is a one-equation linear eddy viscosity model that was derived from two-equation k-\omega closure. It combines the most desirable characteristics of the one-equation k-\epsilon model and one-equation k-\omega model, analogous to the SST k-\omega model which combines best features of two-equation k-\epsilon and k-\omega models.

WA Model (WA 2017m)

The turbulent eddy viscosity is given by:


{{\mu }_{t}}=\rho {{f}_{\mu }}R


The model solves for the variable 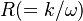R (= k / \omega) using the following equation:


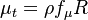
\begin{matrix} \frac{\partial R}{\partial t}+\frac{\partial u_{j} R}{\partial x_{j}}=& \frac{\partial}{\partial x_{j}}\left[\left(\sigma_{R} R+v\right) \frac{\partial R}{\partial x_{j}}\right]+C_{1} R S+f_{1} C_{2 k \omega} \frac{R}{S} \frac{\partial R}{\partial x_{j}} \frac{\partial S}{\partial x_{j}}\\ &-\left(1-f_{1}\right) \min \left[C_{2 k \varepsilon} R^{2}\left(\frac{\frac{\partial S}{\partial x_{j}} \frac{\partial S}{\partial x_{j}}}{S^{2}}\right), C_{m} \frac{\partial R}{\partial x_{j}} \frac{\partial R}{\partial x_{j}}\right] \end{matrix}


Where:


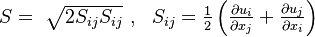
\begin{matrix} S=~\sqrt{2{{S}_{ij}}{{S}_{ij}}}~,~~{{S}_{ij}}=\frac{1}{2}\left( \frac{\partial {{u}_{i}}}{\partial {{x}_{j}}}+\frac{\partial {{u}_{j}}}{\partial {{x}_{i}}} \right) \end{matrix}
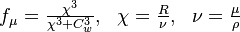
\begin{matrix} {{f}_{\mu }}=\frac{{{\chi }^{3}}}{{{\chi }^{3}}+C_{w}^{3}},~~\chi =\frac{R}{\nu },~~\nu =\frac{\mu }{\rho } \end{matrix}


\begin{matrix} {{f}_{1}}=\min \left( \tanh \left( arg_{1}^{4} \right),0.9 \right),~~ar{{g}_{1}}=\frac{1+\frac{d\sqrt{RS}}{\nu }}{1+{{\left[ \frac{max\left( d\sqrt{RS},1.5R \right)}{20\nu } \right]}^{2}}} \end{matrix}


and d is the minimum distance to the nearest wall. The model constants are:


{{C}_{1k\omega }}=0.0829
{{C}_{1k\varepsilon }}=0.1127
{{C}_{1}}={{f}_{1}}\left( {{C}_{1k\omega }}-{{C}_{1k\varepsilon }} \right)+{{C}_{1k\varepsilon }}
{{\sigma }_{k\omega }}=0.72
{{\sigma }_{k\varepsilon }}=1.0
{{C}_{2k\omega }}=\frac{{{C}_{1k\omega }}}{{{\kappa }^{2}}}+{{\sigma }_{kw}}
{{C}_{2k\varepsilon }}=\frac{{{C}_{1k\varepsilon }}}{{{\kappa }^{2}}}+{{\sigma }_{k\varepsilon }}
\kappa =0.41
{{C}_{w}}=8.54
C_{m} = 8.0

Boundary Conditions

Solid smooth wall:

{{R}_{wall}}=0

Freestream:

{{R}_{farfield}}=3{{v}_{\infty }}:to:5{{v}_{\infty }}

References

  • X. Han, T. J. Wray, and R. K. Agarwal. (2017), "Application of a New DES Model Based on Wray-Agarwal Turbulence Model for Simulation of Wall-Bounded Flows with Separation", AIAA Paper 2017-3966, June 2017.
Retrieved from "https://openfoam.cfd-online.com/Wiki/Wray-Agarwal(WA)_Turbulence_Model"
My wiki