Reynolds stress model (RSM)

From CFD-Wiki

(Difference between revisions)

Revision as of 19:37, 16 April 2017

Introduction

The Reynolds Stress Models (RSM), also known as the Reynolds Stress Transport (RST) models, are higher level, elaborate turbulence models. The method of closure employed is usually called a Second Order Closure. This modelling approach originates from the works by Chou (1945) and Rotta (1951). In Reynolds Stress Models, the eddy viscosity approach is avoided and the individual components of the Reynolds stress tensor are directly computed. These models rely on the exact Reynolds stress transport equation. They are able to account for complex interactions in turbulent flow fields, such as the directional effects of the Reynolds stresses.

Equations

The Reynolds stress model involves calculation of the individual Reynolds stresses, 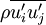$\rho\overline{u'_iu'_j}$ , using differential transport equations. The individual Reynolds stresses are then used to obtain closure of the Reynolds-averaged momentum equation.

The exact transport equations for the transport of the Reynolds stresses, 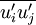$\overline{u'_iu'_j}$ , may be written as follows:

$\frac{\partial}{\partial t}\left(\rho \overline{u'_iu'_j}\right) + \frac{\partial}{\partial x_{k}}\left(\rho u_{k} \overline{u'_iu'_j}\right) = - \frac{\partial}{\partial x_k}\left[\rho \overline{u'_iu'_ju'_k} + \overline{p'\left(\delta_{kj}u'_i + \delta_{ik}u'_j\right)}\right]$

$+ \frac{\partial}{\partial x_k}\left[{\mu \frac{\partial}{\partial x_k}\left(\overline{u'_iu'_j}\right)}\right] - \rho\left(\overline{u'_iu'_k}\frac{\partial u_j}{\partial x_k}+\overline{u'_ju'_k}\frac{\partial u_i}{\partial x_k}\right) - \rho\beta\left(g_i\overline{u'_j\theta}+g_j\overline{u'_i\theta}\right)$

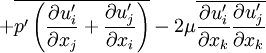
$+ \overline{p'\left(\frac{\partial u'_i}{\partial x_j} + \frac{\partial u'_j}{\partial x_i}\right)} - 2\mu\overline{\frac{\partial u'_i}{\partial x_k} \frac{\partial u'_j}{\partial x_k}}$

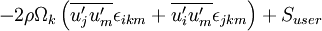
$-2\rho\Omega_k\left(\overline{u'_ju'_m}\epsilon_{ikm} + \overline{u'_iu'_m}\epsilon_{jkm}\right) + S_{user}$

or

Local Time Derivate + 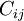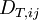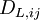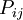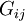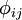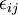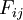$C_{ij}$ = $D_{T,ij}$ + $D_{L,ij}$ + $P_{ij}$ + $G_{ij}$ + $\phi_{ij}$ - $\epsilon_{ij}$ + $F_{ij}$ + User-Defined Source Term

where 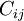$C_{ij}$ is the Convection-Term, 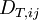$D_{T,ij}$ equals the Turbulent Diffusion, 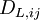$D_{L,ij}$ stands for the Molecular Diffusion, 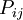$P_{ij}$ is the term for Stress Production, 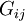$G_{ij}$ equals Buoyancy Production, 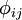$\phi_{ij}$ is for the Pressure Strain, 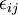$\epsilon_{ij}$ stands for the Dissipation and 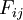$F_{ij}$ is the Production by System Rotation.

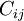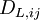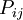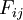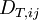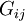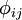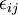Of these terms, $C_{ij}$ , $D_{L,ij}$ , $P_{ij}$ , and $F_{ij}$ do not require modeling. After all, $D_{T,ij}$ , $G_{ij}$ , $\phi_{ij}$ , and $\epsilon_{ij}$ have to be modeled for closing the equations.

Modeling Turbulent Diffusive Transport

Modeling the Pressure-Strain Term

Effects of Buoyancy on Turbulence

Modeling the Turbulence Kinetic Energy

Modeling the Dissipation Rate

Modeling the Turbulent Viscosity

Boundary Conditions for the Reynolds Stresses

Convective Heat and Mass Transfer Modeling

Return-to-isotropy models

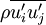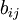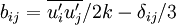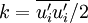For an anisotropic turbulence, the Reynolds stress tensor, $\rho\overline{u'_iu'_j}$ , is usually anisotropic. The second and third invariances of the Reynolds-stress anisotropic tensor $b_{ij}$ are nontrivial, where $b_{ij}=\overline{u'_iu'_j}/2k-\delta_{ij} /3$ and $k = \overline{u'_iu'_i}/2$ . It is naturally to suppose that the anisotropy of the Reynolds-stress tensor results from the anisotropy of turbulent production, dissipation, transport, pressure-stain-rate, and the viscous diffusive tensors. The Reynolds-stress tensor returns to isotropy when the anisotropy of these turbulent components return to isotropy. Such a correlation is described by the Reynolds stress transport equation. Based on these consideration, a number of turbulent models, such as Rotta's model and Lumley's return-to-isotropy model, have been established.

Rotta's model describes the linear return-to-isotropy behavior of a low Reynolds number homogenous turbulence in which the turbulent production, transport, and rapid pressure-strain-rate are negligible. The turbulence dissipation and slow pressure-strain-rate

are preponderant. Under these cirsumstance, Rotta suggested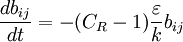 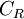$\frac{d b_{ij}}{dt}=-(C_{R}-1) \frac{\varepsilon}{k} b_{ij}$ . Here, $C_{R}$ is called the Rotta constant.

Model constants

The constants suggested for use in this model are as follows:

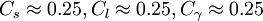
$C_s \approx 0.25, C_l \approx 0.25, C_\gamma \approx 0.25$

Model variants

LRR, Launder-Reece-Rodi

Launder, B. E., Reece, G. J. and Rodi, W. (1975), "Progress in the Development of a Reynolds-Stress Turbulent Closure.", Journal of Fluid Mechanics, Vol. 68(3), pp. 537-566.

SSG, Speziale-Sarkar-Gatski

Speziale, C.G., Sarkar, S., Gatski, T.B. (1991), "Modeling the Pressure-Strain Correlation of Turbulence: an Invariant Dynamical Systems Approach", Journal of Fluid Mechanics, Vol. 227, pp. 245-272.

Performance, applicability and limitations

Implementation issues

References

Chou, P. (1945), "On velocity correlations and the solutions of the equations of turbulent fluctuation.", Quarterly of Applied Mathematics, Vol. 3(1), pp. 38-54.

Rotta, J. (1951), "Statistische theorie nichthomogener turbulenz.", Zeitschrift für Physik A, Vol. 129(6), pp. 547-572.