Diffusion term
From CFD-Wiki
(Difference between revisions)
| Line 13: | Line 13: | ||
[[Image:Nm_descretisation_diffusionterms_01.jpg]] <br> | [[Image:Nm_descretisation_diffusionterms_01.jpg]] <br> | ||
'''Figure 1.1''' <br> | '''Figure 1.1''' <br> | ||
| - | + | <math> \vec r_{0} </math> and <math> \vec r_{1} </math> are position vector of centroids of cells cell 0 and cell 1 respectively. <br> | |
<math> {\rm{d\vec s}} = \vec r_{1} - \vec r_{0} </math> | <math> {\rm{d\vec s}} = \vec r_{1} - \vec r_{0} </math> | ||
| - | |||
<br> | <br> | ||
| + | |||
| + | We wish to approaximate <math> D_f = \Gamma _f \nabla \phi _f \bullet {\rm{\vec A}} </math> at the face. | ||
| + | |||
===2. Approach 1 === | ===2. Approach 1 === | ||
| Line 23: | Line 25: | ||
\vec \alpha {\rm{ = }}\frac{{{\rm{\vec A}}}}{{{\rm{\vec A}} \bullet {\rm{d\vec s}}}} | \vec \alpha {\rm{ = }}\frac{{{\rm{\vec A}}}}{{{\rm{\vec A}} \bullet {\rm{d\vec s}}}} | ||
</math> | </math> | ||
| + | |||
| + | giving us the expression: <br> | ||
| + | :<math> | ||
| + | D_f = \Gamma _f \nabla \phi _f \bullet {\rm{\vec A = }}\Gamma _{\rm{f}} \left[ {\left( {\phi _1 - \phi _0 } \right)\vec \alpha \bullet {\rm{\vec A + }}\bar \nabla \phi \bullet {\rm{\vec A - }}\left( {\bar \nabla \phi \bullet {\rm{d\vec s}}} \right)\vec \alpha \bullet {\rm{\vec A}}} \right] | ||
| + | </math> <br> | ||
| + | where <math> \bar \nabla \phi _f </math> and <math> \Gamma _f </math> are suitable face averages. <br> | ||
Revision as of 22:56, 14 September 2005
Contents |
Discretisation of Diffusive Term
Sub-topics
- Approximation Schemes for diffusive term
- Approximation of Diffusive Fluxes
- Discretisation on orthogonal grids
- Discretisation on non-orthogonal curvilinear body-fitted grids
1. Description
A control volume in mesh is made up of set of faces enclosing it. The figure 1.1 shows a typical situation. Where A represent the magnitude of area of the face. And n represents the normal unit vector of the face under consideration.
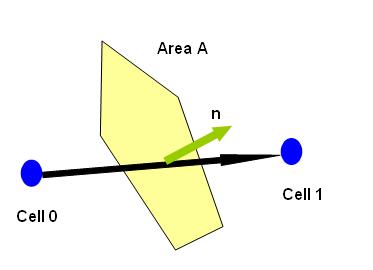
Figure 1.1
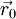 and
and 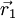 are position vector of centroids of cells cell 0 and cell 1 respectively.
are position vector of centroids of cells cell 0 and cell 1 respectively.
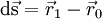
We wish to approaximate 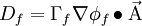 at the face.
at the face.
2. Approach 1
We define vector
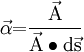
giving us the expression:
where 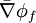 and
and 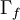 are suitable face averages.
are suitable face averages.

![D_f = \Gamma _f \nabla \phi _f \bullet {\rm{\vec A = }}\Gamma _{\rm{f}} \left[ {\left( {\phi _1 - \phi _0 } \right)\vec \alpha \bullet {\rm{\vec A + }}\bar \nabla \phi \bullet {\rm{\vec A - }}\left( {\bar \nabla \phi \bullet {\rm{d\vec s}}} \right)\vec \alpha \bullet {\rm{\vec A}}} \right]](/W/images/math/7/7/2/772b96059e9032fc07b25c0dee76db6c.png)