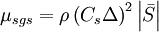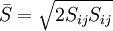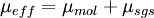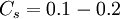Smagorinsky-Lilly model
From CFD-Wiki
(Difference between revisions)
OucapAspas (Talk | contribs) (cvigetno) |
m (Grammatical correction) |
||
| (One intermediate revision not shown) | |||
| Line 1: | Line 1: | ||
| - | + | The Smagorinsky model could be summarised as: | |
| - | The Smagorinsky model could be | + | |
:<math> | :<math> | ||
\tau _{ij} - \frac{1}{3}\tau _{kk} \delta _{ij} = - 2\left( {C_s \Delta } \right)^2 \left| {\bar S} \right|S_{ij} | \tau _{ij} - \frac{1}{3}\tau _{kk} \delta _{ij} = - 2\left( {C_s \Delta } \right)^2 \left| {\bar S} \right|S_{ij} | ||
Latest revision as of 19:42, 19 June 2009
The Smagorinsky model could be summarised as:
In the Smagorinsky-Lilly model, the eddy viscosity is modeled by
Where the filter width is usually taken to be
and
The effective viscosity is calculated from
The Smagorinsky constant usually has the value: