A roughness-dependent model
From CFD-Wiki
(→Algebraic eddy viscosity model [Absi (2006)]) |
(→The mean velocity profile) |
||
| (13 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
| - | ==Two-equation eddy viscosity model== | + | ==Two-equation <math>k</math>-<math>\epsilon</math> eddy viscosity model== |
<table width="70%"><tr><td> | <table width="70%"><tr><td> | ||
<math> | <math> | ||
| - | \nu _t = C_{\mu} {{k^2 } \over \ | + | \nu _t = C_{\mu} {{k^2 } \over \epsilon } |
</math></td><td width="5%">(1)</td></tr></table> | </math></td><td width="5%">(1)</td></tr></table> | ||
where: | where: | ||
<math> C_{\mu} = 0.09 </math> | <math> C_{\mu} = 0.09 </math> | ||
| + | |||
| + | [http://www.cfd-online.com/Wiki/Standard_k-epsilon_model <math>k</math>-<math>\epsilon</math> model] | ||
==One-equation eddy viscosity model== | ==One-equation eddy viscosity model== | ||
| Line 12: | Line 14: | ||
\nu _t = k^{{1 \over 2}} l | \nu _t = k^{{1 \over 2}} l | ||
</math></td><td width="5%">(2)</td></tr></table> | </math></td><td width="5%">(2)</td></tr></table> | ||
| + | |||
| + | [http://www.cfd-online.com/Wiki/Prandtl%27s_one-equation_model One-equation model] | ||
==Algebraic eddy viscosity model== | ==Algebraic eddy viscosity model== | ||
| Line 20: | Line 24: | ||
<math>l_m</math> is the mixing length. | <math>l_m</math> is the mixing length. | ||
| - | ===Algebraic model for the turbulent kinetic | + | ===Algebraic model for the turbulent kinetic energy=== |
<table width="70%"><tr><td> | <table width="70%"><tr><td> | ||
<math> | <math> | ||
k^{{1 \over 2}}(y) = {1 \over {C_{\mu}}^{{1 \over 4}}} u_\tau e^{\frac{-y}{A}} | k^{{1 \over 2}}(y) = {1 \over {C_{\mu}}^{{1 \over 4}}} u_\tau e^{\frac{-y}{A}} | ||
</math></td><td width="5%">(4)</td></tr></table> | </math></td><td width="5%">(4)</td></tr></table> | ||
| - | <math>u_\tau </math> is the shear velocity and <math>A</math> a model parameter. | + | <math>u_\tau </math> is the shear velocity and <math>A</math> a model parameter. |
| + | |||
| + | For steady open channel flows in local equilibrium, where the energy production is balanced by the dissipation, from the modeled <math>k</math>-equation [[#References|[Nezu and Nakagawa (1993)]]] obtained a similar semi-theoretical equation. | ||
| + | |||
| + | ===Algebraic model for the mixing length=== | ||
| + | |||
| + | For local equilibrium, an extension of von Kármán’s similarity hypothesis allows to write, with equation (4) [[#References|[Absi (2006)]]]: | ||
| - | |||
<table width="70%"><tr><td> | <table width="70%"><tr><td> | ||
<math> | <math> | ||
l_m(y) = \kappa \left( A - \left(A - y_0\right) e^{\frac{-(y-y_0)}{A}} \right) | l_m(y) = \kappa \left( A - \left(A - y_0\right) e^{\frac{-(y-y_0)}{A}} \right) | ||
</math></td><td width="5%">(5)</td></tr></table> | </math></td><td width="5%">(5)</td></tr></table> | ||
| - | <math>\kappa = 0.4</math>, <math>y_0</math> is the hydrodynamic roughness | + | <math>\kappa = 0.4</math>, <math>y_0</math> is the hydrodynamic roughness. |
| + | For a smooth wall (<math>y_0 = 0</math>): | ||
| + | <table width="70%"><tr><td> | ||
| + | <math> | ||
| + | l_m(y) = \kappa A \left( 1 - e^{\frac{-y}{A}} \right) | ||
| + | </math></td><td width="5%">(6)</td></tr></table> | ||
===the algebraic eddy viscosity model is therefore=== | ===the algebraic eddy viscosity model is therefore=== | ||
| Line 39: | Line 53: | ||
\nu _t(y) = \kappa \left( A - \left(A - y_0\right) e^{\frac{-(y-y_0)}{A}} \right) | \nu _t(y) = \kappa \left( A - \left(A - y_0\right) e^{\frac{-(y-y_0)}{A}} \right) | ||
u_\tau e^{\frac{-y}{A}} | u_\tau e^{\frac{-y}{A}} | ||
| - | </math></td><td width="5%">( | + | </math></td><td width="5%">(7)</td></tr></table> |
| + | |||
| + | |||
| + | ==The mean velocity profile== | ||
| + | |||
| + | For local equilibrium, we are able to find the mean velocity profile <math>u</math> from the turbulent kinetic energy <math>k</math> (equation 4) and the mixing length <math>l_m</math> (equation 5), by: | ||
| + | <table width="70%"><tr><td> | ||
| + | <math> | ||
| + | {{d u} \over {d y}} = C_{\mu}^{1 \over 4} {{k^{1 \over 2}} \over {l_m}} | ||
| + | </math></td><td width="5%">(8)</td></tr></table> | ||
| + | |||
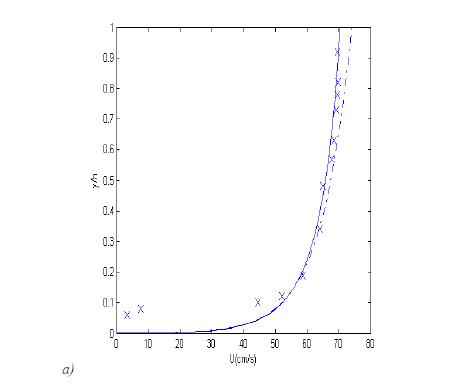
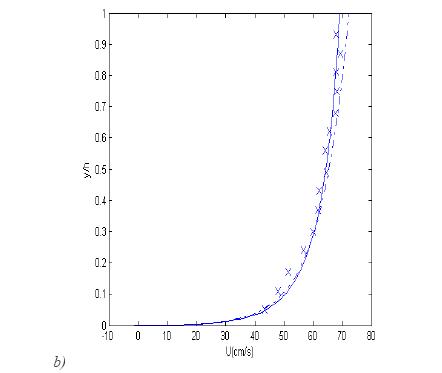
| + | Figure (1) shows that the velocity profile obtained from equations (8), (4) and (5) (solid line) is more accurate than the logarithmic velocity profile (dash-dotted line). | ||
| + | |||
| + | [[Image:fig7a.jpg]] | ||
| + | [[Image:fig7b.jpg]] | ||
| + | |||
| + | '''Figure 1''', Vertical distribution of mean flow velocity. | ||
| + | <math>A = {{h} \over {c_1}}</math>; <math>c_1 = 1</math>; | ||
| + | Dash-dotted line: logarithmic profile; solid line: obtained from equation (8); symbols: experimental data ([[#References|[Sukhodolov ''et al.'' (1998)]]]). a) profile 2: <math>y_0 = 0.062 cm</math>; <math>h = 145 cm</math>; <math>u_\tau = 3.82 cm/s</math>. b) profile 4: <math>y_0 = 0.113 cm</math>; <math>h = 164.5 cm</math>; <math>u_\tau = 3.97 cm/s</math> ; (values of <math>y_0 , h, u_\tau</math> are from [[#References|[Sukhodolov ''et al.'' (1998)]]]); Figure from [[#References|[Absi (2006)]]]. | ||
== References == | == References == | ||
| - | * {{reference-paper|author=Absi, R. |year=2006|title=A roughness and time dependent mixing length equation|rest=Journal of Hydraulic, Coastal and Environmental Engineering | + | * {{reference-paper|author=Absi, R. |year=2006|title=[http://www.jstage.jst.go.jp/article/jscejb/62/4/62_437/_article A roughness and time dependent mixing length equation]|rest=''Journal of Hydraulic, Coastal and Environmental Engineering, (Doboku Gakkai Ronbunshuu B),'' Japan Society of Civil Engineers, Vol. '''62''', No. 4, pp.437-446}} |
| + | |||
| + | * {{reference-paper|author=Nezu, I. and Nakagawa, H. |year=1993|title=Turbulence in open-channel flows|rest=A.A. Balkema, Ed. Rotterdam, The Netherlands}} | ||
| + | |||
| + | * {{reference-paper|author=Sukhodolov, A., Thiele, M. and Bungartz, H. |year=1998|title=Turbulence structure in a river reach with sand bed|rest=''Water Resour. Res.'', Vol. '''34''', pp. 1317-1334}} | ||
| + | |||
[[Category:Turbulence models]] | [[Category:Turbulence models]] | ||
{{stub}} | {{stub}} | ||
Latest revision as of 12:47, 22 June 2007
Contents |
Two-equation 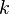 -
- eddy viscosity model
eddy viscosity model
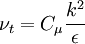 | (1) |
where:
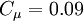
One-equation eddy viscosity model
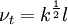 | (2) |
Algebraic eddy viscosity model
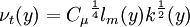 | (3) |
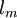 is the mixing length.
is the mixing length.
Algebraic model for the turbulent kinetic energy
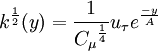 | (4) |
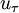 is the shear velocity and
is the shear velocity and 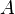 a model parameter.
a model parameter.
For steady open channel flows in local equilibrium, where the energy production is balanced by the dissipation, from the modeled 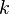 -equation [Nezu and Nakagawa (1993)] obtained a similar semi-theoretical equation.
-equation [Nezu and Nakagawa (1993)] obtained a similar semi-theoretical equation.
Algebraic model for the mixing length
For local equilibrium, an extension of von Kármán’s similarity hypothesis allows to write, with equation (4) [Absi (2006)]:
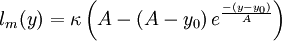 | (5) |
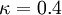 ,
, 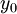 is the hydrodynamic roughness.
For a smooth wall (
is the hydrodynamic roughness.
For a smooth wall (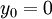 ):
):
 | (6) |
the algebraic eddy viscosity model is therefore
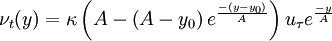 | (7) |
The mean velocity profile
For local equilibrium, we are able to find the mean velocity profile 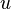 from the turbulent kinetic energy
from the turbulent kinetic energy 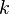 (equation 4) and the mixing length
(equation 4) and the mixing length 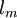 (equation 5), by:
(equation 5), by:
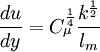 | (8) |
Figure (1) shows that the velocity profile obtained from equations (8), (4) and (5) (solid line) is more accurate than the logarithmic velocity profile (dash-dotted line).
Figure 1, Vertical distribution of mean flow velocity.
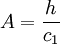 ;
; 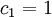 ;
Dash-dotted line: logarithmic profile; solid line: obtained from equation (8); symbols: experimental data ([Sukhodolov et al. (1998)]). a) profile 2:
;
Dash-dotted line: logarithmic profile; solid line: obtained from equation (8); symbols: experimental data ([Sukhodolov et al. (1998)]). a) profile 2: 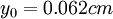 ;
; 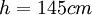 ;
; 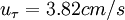 . b) profile 4:
. b) profile 4: 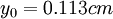 ;
; 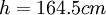 ;
;  ; (values of
; (values of  are from [Sukhodolov et al. (1998)]); Figure from [Absi (2006)].
are from [Sukhodolov et al. (1998)]); Figure from [Absi (2006)].
References
- Absi, R. (2006), "A roughness and time dependent mixing length equation", Journal of Hydraulic, Coastal and Environmental Engineering, (Doboku Gakkai Ronbunshuu B), Japan Society of Civil Engineers, Vol. 62, No. 4, pp.437-446.
- Nezu, I. and Nakagawa, H. (1993), "Turbulence in open-channel flows", A.A. Balkema, Ed. Rotterdam, The Netherlands.
- Sukhodolov, A., Thiele, M. and Bungartz, H. (1998), "Turbulence structure in a river reach with sand bed", Water Resour. Res., Vol. 34, pp. 1317-1334.