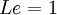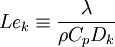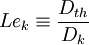Lewis number
From CFD-Wiki
(Difference between revisions)
m (Reverted edits by NorelPasvi (Talk) to last version by Salva) |
|||
| (3 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
The Lewis number for a given species <math> k </math> is | The Lewis number for a given species <math> k </math> is | ||
:<math> | :<math> | ||
| - | Le_k | + | Le_k \equiv \frac{\lambda}{\rho C_p D_k} |
</math> | </math> | ||
Denoting <math> D_{th}= \lambda / \rho C_p </math> the heat diffusivity coefficient the Lewis number | Denoting <math> D_{th}= \lambda / \rho C_p </math> the heat diffusivity coefficient the Lewis number | ||
can be expressed as | can be expressed as | ||
:<math> | :<math> | ||
| - | Le_k | + | Le_k \equiv \frac{D_{th}}{ D_k} |
</math> | </math> | ||
which is the ratio of the heat diffusion speed to the diffusion speed of species <math> k </math>. | which is the ratio of the heat diffusion speed to the diffusion speed of species <math> k </math>. | ||
In many combustion models, all species are assumed to diffuse at the same speed and therefore | In many combustion models, all species are assumed to diffuse at the same speed and therefore | ||
| - | <math> Le=1 </math> | + | <math> Le = 1 </math> |
[[Category:Dimensionless parameters]] | [[Category:Dimensionless parameters]] | ||
Latest revision as of 09:55, 17 December 2008
The Lewis number for a given species  is
is
Denoting 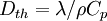 the heat diffusivity coefficient the Lewis number
can be expressed as
the heat diffusivity coefficient the Lewis number
can be expressed as
which is the ratio of the heat diffusion speed to the diffusion speed of species 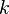 .
.
In many combustion models, all species are assumed to diffuse at the same speed and therefore