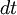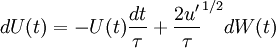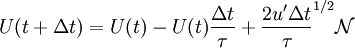Langevin equation
From CFD-Wiki
(Difference between revisions)
| (3 intermediate revisions not shown) | |||
| Line 6: | Line 6: | ||
where <math> dW(t) </math> is a Wiener process. | where <math> dW(t) </math> is a Wiener process. | ||
| - | <math> u' </math> is the turbulence intensity and math> \tau </math> | + | <math> u' </math> is the turbulence intensity and <math> \tau </math> a Lagrangian time-scale. |
Th finite difference approximation of the above equation is | Th finite difference approximation of the above equation is | ||
| Line 18: | Line 18: | ||
The Wiener process can be understood as Gaussian random variable with 0 mean | The Wiener process can be understood as Gaussian random variable with 0 mean | ||
and variance <math> dt</math> | and variance <math> dt</math> | ||
| + | |||
| + | {{Stub}} | ||
Latest revision as of 14:30, 15 June 2007
The stochastic differential equation (SDE) for velocity component 
,
the Langevin equation is
where 
is a Wiener process.
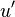is the turbulence intensity and 
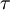a Lagrangian time-scale.
Th finite difference approximation of the above equation is
where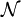 
is a standardized Gaussian random variable with 0 mean an unity variance
which is independent of 
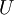on all other time steps (Pope 1994).
The Wiener process can be understood as Gaussian random variable with 0 mean
and variance 
