Incomplete LU factorization - ILU
From CFD-Wiki
(Difference between revisions)
m (Reverted edits by DelbaScaze (Talk) to last version by Tsaad) |
|||
| (8 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
== Algorithm ILU == | == Algorithm ILU == | ||
| - | Algorithm for computing ILU for a n by n matrix A is given by <br> | + | Algorithm for computing ILU for a '''n''' by '''n''' matrix '''A''' is given by <br> |
| + | ---- | ||
| - | + | : for r:= 1 step 1 until n-1 do | |
| - | + | :: d := 1/ a<sub>rr</sub> <br> | |
| - | + | :: for i := (r+1) step 1 until n do <br> | |
| - | + | :: if (i,r)<math>\in</math>S then <br> | |
| - | + | ::: e := da<sub>i,r</sub>; <br> | |
| - | + | ::: a<sub>i,r</sub> := e ; <br> | |
| - | + | ::: for j := (r+1) step 1 until n do <br> | |
| - | + | :::: if ( (i,j)<math>\in</math>S ) and ( (r,j)<math>\in</math>S ) then <br> | |
| - | + | :::: a<sub>i,j</sub> := a<sub>i,j</sub> - e a<sub>r,j</sub> <br> | |
| - | + | :::: end if <br> | |
| - | + | ::: end (j-loop) <br> | |
| - | + | :: end if <br> | |
| - | + | :: end (i-loop) <br> | |
| - | + | : end (r-loop) <br> | |
| + | ---- | ||
| - | + | Here S represents the set of elements of matrix A. The same algorithm could be applied to full matrix A. | |
| - | Here S represents the set of elements of matrix A. | + | |
== Reference == | == Reference == | ||
| - | ''Tony F. Chan and Hank A. Van Der Vorst'' , Approaximate and Incomplete Factorizations | + | '''Tony F. Chan and Hank A. Van Der Vorst''' , "Approaximate and Incomplete Factorizations" |
| + | |||
| + | |||
| + | ---- | ||
| + | <i> Return to [[Numerical methods | Numerical Methods]] </i> | ||
Latest revision as of 12:38, 19 December 2008
Algorithm ILU
Algorithm for computing ILU for a n by n matrix A is given by
- for r:= 1 step 1 until n-1 do
- d := 1/ arr
- for i := (r+1) step 1 until n do
- if (i,r)
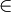S then
- e := dai,r;
- ai,r := e ;
- for j := (r+1) step 1 until n do
- if ( (i,j)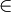S ) and ( (r,j)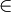S ) then
- ai,j := ai,j - e ar,j
- end if
- if ( (i,j)
- end (j-loop)
- e := dai,r;
- end if
- end (i-loop)
- d := 1/ arr
- end (r-loop)
Here S represents the set of elements of matrix A. The same algorithm could be applied to full matrix A.
Reference
Tony F. Chan and Hank A. Van Der Vorst , "Approaximate and Incomplete Factorizations"
Return to Numerical Methods
