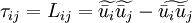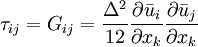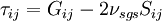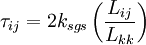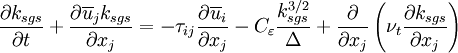Structural modeling
From CFD-Wiki
| (6 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
| - | Those that use the physical hypothesis of scale similarity | + | 1. Those that use the physical hypothesis of scale similarity (Bardina et. al., 1980) |
:<math> | :<math> | ||
| Line 6: | Line 6: | ||
| - | Those derived by formal series expansions | + | 2. Those derived by formal series expansions (Clark et. al., 1979) |
:<math> | :<math> | ||
| Line 12: | Line 12: | ||
</math> | </math> | ||
| - | Mixed models, which are based on linear combinations of the eddy-viscosity and structural types | + | 3. Mixed models, which are based on linear combinations of the eddy-viscosity and structural types |
:<math> | :<math> | ||
| Line 22: | Line 22: | ||
</math> | </math> | ||
| - | Dynamic structure models | + | 4. Dynamic structure models, which divide the modeled SGS stress into a model for the SGS kinetic energy and a model for the structure of the SGS stress tensor (relative weights of each of the components) (Pomraning and Rutland, 2002; Lu et. al. 2007, 2008; Lu and Porte-Agel, 2010) |
:<math> | :<math> | ||
| - | \tau_{ij} = 2k_{sgs} \frac{L_{ij}}{L_{kk}} | + | \tau_{ij} = 2k_{sgs} \left(\frac{L_{ij}}{L_{kk}}\right) |
</math> | </math> | ||
or | or | ||
:<math> | :<math> | ||
| - | \tau_{ij} = 2k_{sgs} \frac{G_{ij}}{G_{kk}} | + | \tau_{ij} = 2k_{sgs} \left(\frac{G_{ij}}{G_{kk}}\right) |
</math> | </math> | ||
| + | The transport equation for the SGS kinetic energy can be used to close the model (Pomraning and Rutland, 2002; Lu et. al., 2008) | ||
| + | :<math> \frac{\partial k_{sgs}}{\partial t} + \frac{\partial \overline u_{j} k_{sgs}} {\partial x_{j}} = - \tau_{ij} \frac{\partial \overline u_{i}}{\partial x_{j}} - C_{\varepsilon} \frac{k_{sgs}^{3/2}}{\Delta} + \frac{\partial}{\partial x_{j}} \left( \nu_t \frac{\partial k_{sgs}}{\partial x_{j}} \right) | ||
| + | </math> | ||
| + | or use a zero-equation procedure (Lu and Porte-Agel, 2010) to estimate the SGS kinetic energy. | ||
| + | |||
| + | == References == | ||
| + | *{{reference-paper|author=J. Bardina and J. H. Ferziger and W. C. Reynolds|year=1980|title=Improved subgrid scale models for large eddy simulation|rest=AIAA Paper No. 80-1357}} | ||
| + | |||
| + | *{{reference-paper|author=R. A. Clark and J. H. Ferziger and W. C. Reynolds|year=1979|title=Evaluation of subgrid-scale models using an accurately simulated turbulent flow|rest=J. Fluid Mech.}} | ||
| + | |||
| + | *{{reference-paper|author=E. Pomraning and C. J. Rutland|year=2002|title=Dynamic one-equation nonviscosity large-eddy simulation model|rest=AIAA J.}} | ||
| + | |||
| + | *{{reference-paper|author=H. Lu and C. J. Rutland and L. M. Smith|year=2007|title=A priori tests of one-equation LES modeling of rotating turbulence|rest=J. Turbul.}} | ||
| + | |||
| + | *{{reference-paper|author=H. Lu and C. J. Rutland and L. M. Smith|year=2008|title=A posteriori tests of one-equation LES modeling of rotating turbulence|rest=Int. J. Mod. Phys. C}} | ||
| + | |||
| + | *{{reference-paper|author=H. Lu and F. Porte-Agel|year=2010|title=A modulated gradient model for large-eddy simulation: application to a neutral atmospheric boundary layer|rest=Phys. Fluids}} | ||
Latest revision as of 20:10, 27 June 2013
1. Those that use the physical hypothesis of scale similarity (Bardina et. al., 1980)
2. Those derived by formal series expansions (Clark et. al., 1979)
3. Mixed models, which are based on linear combinations of the eddy-viscosity and structural types
or
4. Dynamic structure models, which divide the modeled SGS stress into a model for the SGS kinetic energy and a model for the structure of the SGS stress tensor (relative weights of each of the components) (Pomraning and Rutland, 2002; Lu et. al. 2007, 2008; Lu and Porte-Agel, 2010)
or
The transport equation for the SGS kinetic energy can be used to close the model (Pomraning and Rutland, 2002; Lu et. al., 2008)
or use a zero-equation procedure (Lu and Porte-Agel, 2010) to estimate the SGS kinetic energy.
References
- J. Bardina and J. H. Ferziger and W. C. Reynolds (1980), "Improved subgrid scale models for large eddy simulation", AIAA Paper No. 80-1357.
- R. A. Clark and J. H. Ferziger and W. C. Reynolds (1979), "Evaluation of subgrid-scale models using an accurately simulated turbulent flow", J. Fluid Mech..
- E. Pomraning and C. J. Rutland (2002), "Dynamic one-equation nonviscosity large-eddy simulation model", AIAA J..
- H. Lu and C. J. Rutland and L. M. Smith (2007), "A priori tests of one-equation LES modeling of rotating turbulence", J. Turbul..
- H. Lu and C. J. Rutland and L. M. Smith (2008), "A posteriori tests of one-equation LES modeling of rotating turbulence", Int. J. Mod. Phys. C.
- H. Lu and F. Porte-Agel (2010), "A modulated gradient model for large-eddy simulation: application to a neutral atmospheric boundary layer", Phys. Fluids.