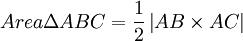Area calculations
From CFD-Wiki
(Difference between revisions)
(→Area of Triangle) |
m (Reverted edits by RoletOchic (Talk) to last version by Zxaar) |
||
| (5 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
== Area of Triangle == | == Area of Triangle == | ||
| - | <p>The area of a triangle made up of three vertices A(x1,y1,z1), B(x2,y2,z2) and C(x3,y3,z3) can be represented <br>by the vector-cross-product of vectors along two sides of the triangle sharing a common vertex. <br>For the above mentioned triangle we have three sides as AB, BC and CA, the area of triangle is given by:<br> | + | <p>The area of a triangle made up of three vertices '''A(x1,y1,z1), B(x2,y2,z2) and C(x3,y3,z3)''' can be represented <br>by the vector-cross-product of vectors along two sides of the triangle sharing a common vertex. <br>For the above mentioned triangle we have three sides as '''AB''', '''BC''' and '''CA''', the area of triangle is given by:<br> |
| - | Area | + | :<math> |
| - | AB = Vector from vertex A to vertex B <br> | + | Area\Delta ABC = {1 \over 2}\left| {AB \times AC} \right| |
| - | AC = Vector from vertex A to vertex C. <br> | + | </math> |
| + | '''AB''' = Vector from vertex A to vertex B. <br> | ||
| + | '''AC''' = Vector from vertex A to vertex C. <br> | ||
| + | |||
</p> | </p> | ||
== Area of Polygonal Surface == | == Area of Polygonal Surface == | ||
<p>A polygon can be divided into triangles sharing a common vertex of the polygon. The total area of the polygon <br>can be approximated by sum of all triangle-areas it is made up of.</p> | <p>A polygon can be divided into triangles sharing a common vertex of the polygon. The total area of the polygon <br>can be approximated by sum of all triangle-areas it is made up of.</p> | ||
| + | |||
| + | ---- | ||
| + | <i> Return to [[Numerical methods | Numerical Methods]] </i> | ||
Latest revision as of 12:31, 19 December 2008
Area of Triangle
The area of a triangle made up of three vertices A(x1,y1,z1), B(x2,y2,z2) and C(x3,y3,z3) can be represented
by the vector-cross-product of vectors along two sides of the triangle sharing a common vertex.
For the above mentioned triangle we have three sides as AB, BC and CA, the area of triangle is given by:
AC = Vector from vertex A to vertex C.
Area of Polygonal Surface
A polygon can be divided into triangles sharing a common vertex of the polygon. The total area of the polygon
can be approximated by sum of all triangle-areas it is made up of.
Return to Numerical Methods