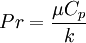Prandtl number
From CFD-Wiki
| (4 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
The Prandtl number is defined as | The Prandtl number is defined as | ||
| - | <math> | + | :<math> |
Pr = \frac{\mu C_p}{k} | Pr = \frac{\mu C_p}{k} | ||
</math> | </math> | ||
| Line 10: | Line 10: | ||
* <math>C_p</math> is the specific heat at constant pressure | * <math>C_p</math> is the specific heat at constant pressure | ||
* <math>k</math> is the coefficient of thermal conduction | * <math>k</math> is the coefficient of thermal conduction | ||
| + | |||
| + | |||
| + | It is the ratio of momentum diffusivity (kinematic viscosity) to thermal diffusivity. It can be related to the thickness of the thermal and velocity boundary layers. It is actually the ratio of velocity boundary layer to thermal boundary layer. When Pr=1, the boundary layers coincide. When Pr is small, it means that heat diffuses very quickly compared to the velocity (momentum). This means the thickness of the thermal boundary layer is much bigger than the velocity boundary layer for liquid metals. | ||
| + | |||
| + | The parameter is named after the German physicist Ludwig Prandtl (1875 - 1953), a pioneer of aerodynamics; developed the mathematical basis for the fundamental principles of subsonic aerodynamics in the earlier 20th century. His studies identified the boundary layer, thin-airfoils, and lifting-line theories. | ||
| + | |||
| + | [[Category: Dimensionless parameters]] | ||
Latest revision as of 04:40, 3 November 2008
The Prandtl number is defined as
where
-
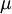is the dynamic viscosity coefficient
-
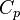is the specific heat at constant pressure
-
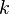is the coefficient of thermal conduction
It is the ratio of momentum diffusivity (kinematic viscosity) to thermal diffusivity. It can be related to the thickness of the thermal and velocity boundary layers. It is actually the ratio of velocity boundary layer to thermal boundary layer. When Pr=1, the boundary layers coincide. When Pr is small, it means that heat diffuses very quickly compared to the velocity (momentum). This means the thickness of the thermal boundary layer is much bigger than the velocity boundary layer for liquid metals.
The parameter is named after the German physicist Ludwig Prandtl (1875 - 1953), a pioneer of aerodynamics; developed the mathematical basis for the fundamental principles of subsonic aerodynamics in the earlier 20th century. His studies identified the boundary layer, thin-airfoils, and lifting-line theories.
