Introduction to turbulence/Stationarity and homogeneity
From CFD-Wiki
(→Processes statistically stationary in time) |
(→Processes statistically stationary in time) |
||
| Line 4: | Line 4: | ||
When the statistical properties of a random process are independent of time, the random process is said to be ''stationary''. For such a process all the moments are time-independent, e.g., <math> \left\langle \tilde{ u \left( t \right)} \right\rangle = U </math>, etc. In fact, the probability density itself is time-independent, as should be obvious from the fact that the moments are time independent. | When the statistical properties of a random process are independent of time, the random process is said to be ''stationary''. For such a process all the moments are time-independent, e.g., <math> \left\langle \tilde{ u \left( t \right)} \right\rangle = U </math>, etc. In fact, the probability density itself is time-independent, as should be obvious from the fact that the moments are time independent. | ||
| + | |||
| + | An alternative way of looking at ''stationarity'' is to note that ''the statistics of the process are independent of the origin in time''. It is obvious from the above, for example, that if the statistics of a process are time independent, then <math> \left\langle u^{n} \left( t \right) \right\rangle = \left\langle u^{n} \left( t + T \right) \right\rangle </math> , etc., where <math> T </math> is some arbitrary translation of the origin in time. Less obvious, but equally true, is that the product <math> \left\langle u \left( t \right) u \left( t' \right) \right\rangle </math> depends only on time difference <math> t'-t </math> and not on <math> t </math> (or <math> t' </math> ) directly. This consequence of stationarity can be extended to any product moment. | ||
== The autocorrelation == | == The autocorrelation == | ||
Revision as of 03:47, 4 January 2008
Processes statistically stationary in time
Many random processes have the characteristic that their statistical properties do not appear to depend directly on time, even though the random variables themselves are time-dependent. For example, consider the signals shown in Figures 2.2 and 2.5
When the statistical properties of a random process are independent of time, the random process is said to be stationary. For such a process all the moments are time-independent, e.g.,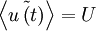 
, etc. In fact, the probability density itself is time-independent, as should be obvious from the fact that the moments are time independent.
An alternative way of looking at stationarity is to note that the statistics of the process are independent of the origin in time. It is obvious from the above, for example, that if the statistics of a process are time independent, then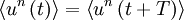 
, etc., where 
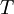is some arbitrary translation of the origin in time. Less obvious, but equally true, is that the product 
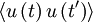depends only on time difference 
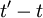and not on 
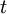(or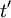 
) directly. This consequence of stationarity can be extended to any product moment.
