2-D vortex in isentropic flow
From CFD-Wiki
(Difference between revisions)
Roberthealy1 (Talk | contribs) m (Provided interlinks between this page and other pages (many may require creation)) |
Roberthealy1 (Talk | contribs) m (I think that this article may qualify as a stub, as it represents a POV; "one choice". An explanation of what the test is and what it can be used for would be worthwhile) |
||
| Line 30: | Line 30: | ||
</math> | </math> | ||
| - | is distance from the [[vortex]] center <math>(x_o, y_o)</math>. One choice for the domain | + | is distance from the [[vortex]] center <math>(x_o, y_o)</math>. |
| - | and parameters | + | |
| + | One choice for the domain and parameters is: | ||
:<math> | :<math> | ||
| Line 45: | Line 46: | ||
*{{reference-paper | author=Yee, H-C., Sandham, N. and Djomehri, M., | year=1999 | title=Low dissipative high order shock-capturing methods using characteristic-based filters| rest=JCP, Vol. 150}} | *{{reference-paper | author=Yee, H-C., Sandham, N. and Djomehri, M., | year=1999 | title=Low dissipative high order shock-capturing methods using characteristic-based filters| rest=JCP, Vol. 150}} | ||
| + | |||
| + | |||
| + | {{stub}} | ||
Revision as of 18:45, 13 August 2007
The test case involves convection of an isentropic vortex in inviscid flow. The free-stream conditions are
Perturbations are added to the free-stream in such a way that there is no entropy gradient in the flow-field. The perturbations are given by
where
is distance from the vortex center 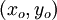 .
.
One choice for the domain and parameters is:
As a result of isentropy, the exact solution corresponds to a pure advection of the vortex at the free-stream velocity. Further details can be found in Yee et al. (1999).
References
- Yee, H-C., Sandham, N. and Djomehri, M., (1999), "Low dissipative high order shock-capturing methods using characteristic-based filters", JCP, Vol. 150.

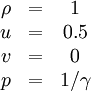
![\begin{matrix}
(\delta u, \delta v) &=& \frac{\beta}{2\pi} \exp\left( \frac{1-r^2}{2}
\right) [ -(y-y_o), (x-x_o) ] \\
\rho &=& \left[ 1 - \frac{ (\gamma-1)\beta^2}{8\gamma\pi} \exp\left(
1-r^2\right) \right]^{\frac{1}{\gamma-1}} \\
p &=& \frac{ \rho^\gamma }{\gamma}
\end{matrix}](/W/images/math/6/9/a/69acee89889dd5a02d5448a3d1e227d2.png)
![r = [ (x-x_o)^2 + (y-y_o)^2 ]^{1/2}](/W/images/math/6/3/5/635b76a00e794bbe4119341445847905.png)
![\Omega = [0,10] \times [-5,5], \quad
(x_o, y_o) = (5,0), \quad
\beta = 5](/W/images/math/c/e/a/ceae1619f8ff0db839e9a7afecbd5f9c.png)