Stencil jumping
From CFD-Wiki
m (stencil jumping algorithm, the underlying principle and the method) |
|||
| (2 intermediate revisions not shown) | |||
| Line 6: | Line 6: | ||
This algorithm finds extensive use in cfd in terms of holecutting and interpolation when two meshes lie one inside the other.The other variations of the problem would be something like this.Given a place, which lattitude and longitude does it lie.The brute force algorithm would find the distance of the point from every mesh point and see which is smallest.Another approach would be to use a binary search algorithm which would yield a result comparable in speed to the stencil jumping algorithm.A combination of both the binary search and the stencil jumping algorithm will yield an optimum result in the minimum possible time. | This algorithm finds extensive use in cfd in terms of holecutting and interpolation when two meshes lie one inside the other.The other variations of the problem would be something like this.Given a place, which lattitude and longitude does it lie.The brute force algorithm would find the distance of the point from every mesh point and see which is smallest.Another approach would be to use a binary search algorithm which would yield a result comparable in speed to the stencil jumping algorithm.A combination of both the binary search and the stencil jumping algorithm will yield an optimum result in the minimum possible time. | ||
| - | '''[[The principle]]''' | + | '''[[Stencil jumping, the principle|The principle]]''' |
| - | [[Image: | + | [[Image:stencil_quad.jpg|300 px]] |
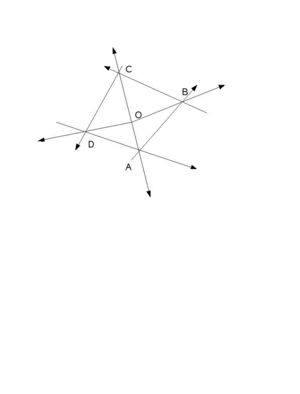
Consider one element of a 2 dimensional mesh, for simplicity and consider a point O inside. | Consider one element of a 2 dimensional mesh, for simplicity and consider a point O inside. | ||
| Line 16: | Line 16: | ||
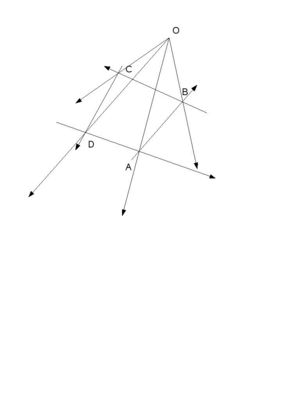
This is not the case when the point is outside. | This is not the case when the point is outside. | ||
| - | [[Image: | + | [[Image:stencil_quad1.jpg|300 px]] |
Here we see that, all the cross products are not positive.This is the major testing criterion in the alogrithm. | Here we see that, all the cross products are not positive.This is the major testing criterion in the alogrithm. | ||
Latest revision as of 07:37, 25 May 2007
Stencil jumping, at times called stencil walking, is an ingenius algorithm by which one will be able to locate the grid element enclosing a given point for any structured mesh.In simple words, given a point and a structured mesh, this algorithm will help you locate the mesh element that will enclose the given point.
This algorithm finds extensive use in cfd in terms of holecutting and interpolation when two meshes lie one inside the other.The other variations of the problem would be something like this.Given a place, which lattitude and longitude does it lie.The brute force algorithm would find the distance of the point from every mesh point and see which is smallest.Another approach would be to use a binary search algorithm which would yield a result comparable in speed to the stencil jumping algorithm.A combination of both the binary search and the stencil jumping algorithm will yield an optimum result in the minimum possible time.
Consider one element of a 2 dimensional mesh, for simplicity and consider a point O inside. The mesh element vertices are denoted by A,B,C and D and the vectors AB,BC,CD,DA,OA,OB,OC and OD are represented. The cross product of OA and AB will yield a vector perpendicular to the plane coming out of the monitor.We say that the cross product is postive.It will be observed that the cross products of OB and BC,OC and CD; and OD and DA are all positive.
This is not the case when the point is outside.
Here we see that, all the cross products are not positive.This is the major testing criterion in the alogrithm.
The algorithm needs a guess to start off.The required cross products are found in the order
1) OA X AB 2) OB X BC 3) OC X CD 4) OD X DA
each of these cross products are checked one by one on who becomes negative first.if OA X AB becomes negative first, the next guess should be one step ahead along DA.if OB X BC is negative move along AB by one step to find the next guess and so on.
The algorithm will converge at the exact grid element where all the cross products are positive.