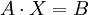Conjugate gradient methods
From CFD-Wiki
(Difference between revisions)
(→Basic Concept) |
(→External links) |
||
| Line 9: | Line 9: | ||
==External links== | ==External links== | ||
* [http://www.math-linux.com/spip.php?article54 Conjugate Gradient Method] by N. Soualem. | * [http://www.math-linux.com/spip.php?article54 Conjugate Gradient Method] by N. Soualem. | ||
| + | * [http://www.math-linux.com/spip.php?article55 Preconditioned Conjugate Gradient Method] by N. Soualem. | ||
---- | ---- | ||
<i> Return to [[Numerical methods | Numerical Methods]] </i> | <i> Return to [[Numerical methods | Numerical Methods]] </i> | ||
Latest revision as of 17:49, 26 August 2006
Basic Concept
For the system of equations:
The unpreconditioned conjugate gradient method constructs the ith iterate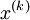 
as an element of 
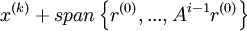so that so that 
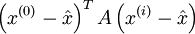is minimized , where 
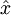is the exact solution of 
.
This minimum is guaranteed to exist in general only if A is symmetric positive definite. The preconditioned version of these methods use a different subspace for constructing the iterates, but it satisfies the same minimization property over different subspace. It requires that the preconditioner M is symmetric and positive definite.
External links
- Conjugate Gradient Method by N. Soualem.
- Preconditioned Conjugate Gradient Method by N. Soualem.
Return to Numerical Methods
