Yap correction
From CFD-Wiki
| Line 27: | Line 27: | ||
The Yap correction is active in nonequilibrium flows and tends to reduce the departure of the turbulence length scale from its local equilibrium level. | The Yap correction is active in nonequilibrium flows and tends to reduce the departure of the turbulence length scale from its local equilibrium level. | ||
| - | Yap showed strongly improved results with the k-epsilon model in separated flows when using this extra source term. Launder [[#References|[Launder, B. E. (1993)]]] also recommends that this term should be used with the epsilon equation. | + | Yap showed strongly improved results with the k-epsilon model in separated flows when using this extra source term. It has also been shown to improve the results in stagnation region. Launder [[#References|[Launder, B. E. (1993)]]] also recommends that this term should always be used with the epsilon equation. |
The Yap source term contains the explicit distance to the nearest wall, <math>y_n</math>. In an unstructured 3D solver this distance is usually not available and it can be ambiguous how to compute it in more complex topologies. This makes the Yap correction most suitable for use in a structured code where the normal wall distance is readily available. | The Yap source term contains the explicit distance to the nearest wall, <math>y_n</math>. In an unstructured 3D solver this distance is usually not available and it can be ambiguous how to compute it in more complex topologies. This makes the Yap correction most suitable for use in a structured code where the normal wall distance is readily available. | ||
Revision as of 14:24, 25 May 2006
The Yap correction consists of a modifification of the epsilon equation in the form of an extra source term, 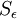 , added to the right hand side of the epsilon equation. The source term can be written as:
, added to the right hand side of the epsilon equation. The source term can be written as:
Where
This source term should be added to the epsilon equation in the following way:
Where the epsilon equation has been written in the same way is in the CFD-Wiki article on low-Re k-epsilon models.
The Yap correction is active in nonequilibrium flows and tends to reduce the departure of the turbulence length scale from its local equilibrium level.
Yap showed strongly improved results with the k-epsilon model in separated flows when using this extra source term. It has also been shown to improve the results in stagnation region. Launder [Launder, B. E. (1993)] also recommends that this term should always be used with the epsilon equation.
The Yap source term contains the explicit distance to the nearest wall,  . In an unstructured 3D solver this distance is usually not available and it can be ambiguous how to compute it in more complex topologies. This makes the Yap correction most suitable for use in a structured code where the normal wall distance is readily available.
. In an unstructured 3D solver this distance is usually not available and it can be ambiguous how to compute it in more complex topologies. This makes the Yap correction most suitable for use in a structured code where the normal wall distance is readily available.
References
Launder, B. E. (1993), "Modelling Convective Heat Transfer in Complex Turbulent Flows", Engineering Turbulence Modeling and Experiments 2, Proceedings of the Second International Symposium, Florence, Italy, 31 May - 2 June 1993, Edited by W. Rodi and F. Martelli, Elsevier, 1993, ISBN 0444898026.
Yap, C. J. (1987), Turbulent Heat and Momentum Transfer in Recirculating and Impinging Flows, PhD Thesis, Faculty of Technology, University of Manchester, United Kingdom.

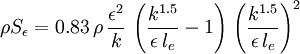

![\frac{\partial}{\partial t} \left( \rho \epsilon \right) +
\frac{\partial}{\partial x_j}
\left[
\rho \epsilon u_j - \left( \mu + \frac{\mu_t}{\sigma_\epsilon} \right)
\frac{\partial \epsilon}{\partial x_j}
\right]
=
\left( C_{\epsilon_1} f_1 P - C_{\epsilon_2} f_2 \rho \epsilon \right)
\frac{\epsilon}{k}
+ \rho E
+ \rho S_\epsilon](/W/images/math/a/7/5/a758d253c1fa5a752e369768c8bacac5.png)