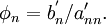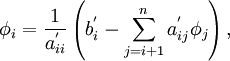Gaussian elimination
From CFD-Wiki
(Difference between revisions)
(capitalized Phi) |
|||
| Line 1: | Line 1: | ||
== Gauss Elimination == | == Gauss Elimination == | ||
| - | We consider the system of linear equations '''<math> A\ | + | We consider the system of linear equations '''<math> A\phi = B </math>''' or <br> |
:<math> | :<math> | ||
\left[ | \left[ | ||
| Line 74: | Line 74: | ||
\begin{matrix} | \begin{matrix} | ||
{b_1^' } \\ | {b_1^' } \\ | ||
| - | { | + | {b_2^' } \\ |
. \\ | . \\ | ||
| - | { | + | {b_n^' } \\ |
\end{matrix} | \end{matrix} | ||
| Line 84: | Line 84: | ||
</math> <br> | </math> <br> | ||
| - | + | The solution to the original system is found via '''back substitution'''. The solution to the last equation is | |
| + | |||
:<math> | :<math> | ||
| - | \ | + | \phi_n = b_n^'/a_{nn}'. |
| - | </math> | + | </math> |
| - | + | ||
| + | This result may now be substituted into the second to last equation, allowing us to solve for <math>\phi_{n-1}</math>. Repetition of this substitution process will give us the complete solution vector. The back substitution process may be expressed as | ||
| + | |||
| + | :<math> | ||
| + | \phi_i = {1 \over {a_{ii}^' }}\left( {b_i^' - \sum\limits_{j = i + 1}^n {a_{ij}^' \phi_j } } \right), | ||
| + | </math> | ||
| - | + | where <math>i=n,n-1,\ldots,1</math>. | |
| - | <i | + | |
Revision as of 22:30, 16 December 2005
Gauss Elimination
We consider the system of linear equations 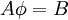 or
or
To perform Gaussian elimination starting with the above given system of equations we compose the augmented matrix equation in the form:
After performing elementary raw operations the augmented matrix is put into the upper triangular form:
The solution to the original system is found via back substitution. The solution to the last equation is
This result may now be substituted into the second to last equation, allowing us to solve for 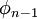 . Repetition of this substitution process will give us the complete solution vector. The back substitution process may be expressed as
. Repetition of this substitution process will give us the complete solution vector. The back substitution process may be expressed as
where 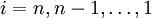 .
.

![\left[
\begin{matrix}
{a_{11} } & {a_{12} } & {...} & {a_{1n} } \\
{a_{21} } & {a_{22} } & . & {a_{21} } \\
. & . & . & . \\
{a_{n1} } & {a_{n1} } & . & {a_{nn} } \\
\end{matrix}
\right]
\left[
\begin{matrix}
{\phi_1 } \\
{\phi_2 } \\
. \\
{\phi_n } \\
\end{matrix}
\right]
=
\left[
\begin{matrix}
{b_1 } \\
{b_2 } \\
. \\
{b_n } \\
\end{matrix}
\right]](/W/images/math/a/4/d/a4dada28dd7a85c53604dc331829fc4e.png)
![\left[
\begin{matrix}
{a_{11} } & {a_{12} } & {...} & {a_{1n} } \\
{a_{21} } & {a_{22} } & . & {a_{21} } \\
. & . & . & . \\
{a_{n1} } & {a_{n1} } & . & {a_{nn} } \\
\end{matrix}
\left|
\begin{matrix}
{b_1 } \\
{b_2 } \\
. \\
{b_n } \\
\end{matrix}
\right.
\right]
\left[
\begin{matrix}
{\phi_1 } \\
{\phi_2 } \\
. \\
{\phi_n } \\
\end{matrix}
\right]](/W/images/math/4/7/e/47e9bee10079eb1421bd67e9bd451eaf.png)
![\left[
\begin{matrix}
{a_{11}^' } & {a_{12}^' } & {...} & {a_{1n}^' } \\
0 & {a_{22}^' } & . & {a_{2n}^' } \\
. & . & . & . \\
0 & 0 & . & {a_{nn}^' } \\
\end{matrix}
\left|
\begin{matrix}
{b_1^' } \\
{b_2^' } \\
. \\
{b_n^' } \\
\end{matrix}
\right.
\right]](/W/images/math/d/c/0/dc0b0d3482afa7d527b8f29f7fd72ea0.png)