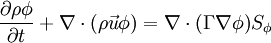Generic scalar transport equation
From CFD-Wiki
| Line 7: | Line 7: | ||
<math> \frac{\partial{\rho u}}{\partial t} + \nabla \cdot (\rho \vec u u ) =\nabla \cdot (\mu \nabla u ) - \frac {\partial p}{\partial x} + B_x + V_x </math> <br> | <math> \frac{\partial{\rho u}}{\partial t} + \nabla \cdot (\rho \vec u u ) =\nabla \cdot (\mu \nabla u ) - \frac {\partial p}{\partial x} + B_x + V_x </math> <br> | ||
where <math> B_x </math> is the body force in the x-direction and <math>V_x</math> includes the viscous terms that are not expressed by <math>\nabla \cdot (\mu \nabla u )</math> <br> | where <math> B_x </math> is the body force in the x-direction and <math>V_x</math> includes the viscous terms that are not expressed by <math>\nabla \cdot (\mu \nabla u )</math> <br> | ||
| + | <br> | ||
| + | Upon inspection of the above equations, it can be infered that all the dependent variables seem to obey a generalized conservation principle. If the dependent variable (scalar or vector) is denoted by <math>\phi</math>, the '''generic''' differential equation is <br> | ||
| + | <math> \frac{\partial{\rho \phi}}{\partial t} + \nabla \cdot (\rho \vec u \phi ) =\nabla \cdot (\Gamma \nabla \phi ) S_{\phi}</math> <br> | ||
Revision as of 21:58, 13 December 2005
A differential equation epxresses a certain conservation principle. Whether be it in electromagnetics, fluid dynamics, heat transfer, radiation, electronics... conservation principles are the basis for the derivation of differential or integro-differential equations. In this respect, any differential equation addresses a certain quantity as it dependent variable and thus expresses the balance between the phenomena affecting the evolution of this quanitity. For example, the temperature of a fluid in a heated pipe is affected by convection due to the solid-fluid interface, and due to the fluid-fluid interaction. Furthermore, temperature is also diffused inside the fluid. For a state state problem, with the absence of sources, a differential equation governing the temperature will definetely express a balance between convection and diffusion.
A brief inspection of the equations governing various physical phenomena will reveal that all of these equations can be put into a generic form thus allowing a systematic approach for a computer simulation.
For example, the conservation equation of a chemical species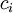 
is
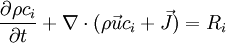where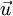 
denotes the velocity field, 
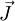denotes the diffusion flux the of the chemical species, and 
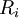denotes the rate of generation of 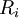caused by the chemical reaction.
The x-momentum equation for a Newtonian fluid can be written as
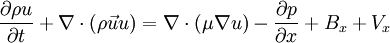
where 
is the body force in the x-direction and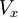 
includes the viscous terms that are not expressed by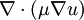 
Upon inspection of the above equations, it can be infered that all the dependent variables seem to obey a generalized conservation principle. If the dependent variable (scalar or vector) is denoted by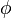 
, the generic differential equation is
