CFD Online Logo CFD Online URL
www.cfd-online.com
[Sponsors]
Home > Wiki > Diffusion term

Diffusion term

From CFD-Wiki

(Difference between revisions)
Jump to: navigation, search
(→Discretisation of the Diffusion Term)
Line 3: Line 3:
=== Description===  
=== Description===  
<br>
<br>
 +
For a general control volume (orthogonal, non-orthogonal), the discretization of the diffusion term can be written in the following form<br>
 +
<math> \int_{S}\Gamma\nabla\phi\cdot{\rm{d\vec S}}  = \sum_{faces}\Gamma _f \nabla \phi _f  \cdot{\rm{\vec S_f}} </math> <br>
 +
where
 +
*S denotes the surface area of the control volume
 +
*<math>S_f</math> denotes the area of a face for the control volume
 +
As usual, the subscript f refers to a given face. The figure below describes the terminology used in the framework of a general non-orthogonal control volume<br>
 +
[[Image:non_orthogonal_CV_terminology.jpg]] <br>
 +
'''A general non-orthogonal control volume''' <br>
 +
Note: The approaches those are discussed here are applicable to non-orthoganal meshes as well as orthogonal meshes.
Note: The approaches those are discussed here are applicable to non-orthoganal meshes as well as orthogonal meshes.
<br>
<br>
-
A control volume in mesh is made up of set of faces enclosing it. The figure 1.1 shows a typical situation. Where '''A''' represent the magnitude of area of the face. And '''n''' represents the normal unit vector of the face under consideration.  
+
A control volume in mesh is made up of set of faces enclosing it. Where '''<math>S_f</math>''' represents the magnitude of area of the face. And '''n''' represents the normal unit vector of the face under consideration.  
-
<br>
+
 
-
[[Image:Nm_descretisation_diffusionterms_01.jpg]] <br>
+
If <math> \vec r_{P} </math> and <math> \vec r_{N} </math> are position vector of centroids of cells P and N respectively. Then, we define <br>
-
'''Figure 1.1''' <br>
+
<math> \overrightarrow{d_{PN}}=  \vec r_{P}  - \vec r_{N}  </math>
-
:<br>
+
 
-
<math> \vec r_{0} </math> and <math> \vec r_{1} </math> are position vector of centroids of cells cell 0 and cell 1 respectively. <br>
+
-
<math> {\rm{d\vec s}} =  \vec r_{1}  - \vec r_{0}  </math>
+
<br>
<br>
-
We wish to approaximate <math> D_f  = \Gamma _f \nabla \phi _f  \bullet {\rm{\vec A}} </math> at the face.
+
We wish to approaximate the diffusive flux <math> D_f  = \Gamma _f \nabla \phi _f  \cdot{\rm{\vec S_f}} </math> at the face.
=== Approach 1 ===
=== Approach 1 ===
-
Another approach is to use a simple expression for estimating the gradient of scalar normal to the face. <br>
+
A first approach is to use a simple expression for estimating the gradient of a scalar normal to the face. <br>
:<math>
:<math>
-
D_f  = \Gamma _f \nabla \phi _f  \bullet \vec A = \Gamma _f \left[ {\left( {\phi _1 - \phi _0 } \right)\left| {{{\vec A} \over {d\vec s}}} \right|} \right]
+
D_f  = \Gamma _f \nabla \phi _f  \cdot \vec S_f = \Gamma _f \left[ {\left( {\phi _N - \phi _P } \right)\left| {{{\vec S_f} \over {\overrightarrow{d_{PN}}}}} \right|} \right]
</math> <br>
</math> <br>
-
where <math> \Gamma _f  </math> is suitable face averages. <br>
+
where <math> \Gamma _f  </math> is a suitable face average. <br>
-
This approach is not very good when the non-orthogonality of the faces increases. Instead for the fairly non-orthogonal meshes, it is advisable to use the following approaches. <br>
+
This approach is not very good when the non-orthogonality of the faces increases. If this is the case, it is advisable to use one of the following approaches. <br>
=== Approach 2 ===
=== Approach 2 ===
-
We define vector
+
We define the vector
<math>
<math>
-
\vec \alpha {\rm{ = }}\frac{{{\rm{\vec A}}}}{{{\rm{\vec A}} \bullet {\rm{d\vec s}}}}
+
\vec \alpha {\rm{ = }}\frac{{{\rm{\vec {S_f}}}}}{{{\rm{\vec S_f}} \cdot {\overrightarrow{d_{PN}}}}}
</math>
</math>
giving us the expression: <br>
giving us the expression: <br>
:<math>
:<math>
-
D_f  = \Gamma _f \nabla \phi _f  \bullet {\rm{\vec A = }}\Gamma _{\rm{f}} \left[ {\left( {\phi _1 - \phi _0 } \right)\vec \alpha  \bullet {\rm{\vec A + }}\bar \nabla \phi \bullet {\rm{\vec A - }}\left( {\bar \nabla \phi \bullet {\rm{d\vec s}}} \right)\vec \alpha  \bullet {\rm{\vec A}}} \right]
+
D_f  = \Gamma _f \nabla \phi _f  \cdot{\rm{\vec S_f = }}\Gamma _{\rm{f}} \left[ {\left( {\phi _N - \phi _P } \right)\vec \alpha  \cdot {\rm{\vec S_f + }}\bar \nabla \phi_f \cdot {\rm{\vec S_f - }}\left( {\bar \nabla \phi_f \cdot {\overrightarrow{d_{PN}}}} \right)\vec \alpha  \cdot {\rm{\vec S_f}}} \right]
</math> <br>
</math> <br>
where <math> \bar \nabla \phi _f  </math> and <math> \Gamma _f  </math> are suitable face averages. <br>
where <math> \bar \nabla \phi _f  </math> and <math> \Gamma _f  </math> are suitable face averages. <br>

Revision as of 04:36, 5 December 2005

Contents

Discretisation of the Diffusion Term

Description


For a general control volume (orthogonal, non-orthogonal), the discretization of the diffusion term can be written in the following form
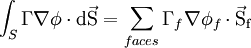
\int_{S}\Gamma\nabla\phi\cdot{\rm{d\vec S}} = \sum_{faces}\Gamma _f \nabla \phi _f \cdot{\rm{\vec S_f}}
where

  • S denotes the surface area of the control volume
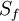  • S_f denotes the area of a face for the control volume

As usual, the subscript f refers to a given face. The figure below describes the terminology used in the framework of a general non-orthogonal control volume
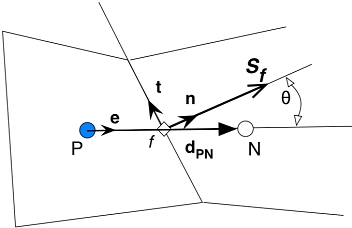
Non orthogonal CV terminology.jpg
A general non-orthogonal control volume

Note: The approaches those are discussed here are applicable to non-orthoganal meshes as well as orthogonal meshes.
A control volume in mesh is made up of set of faces enclosing it. Where 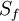S_f represents the magnitude of area of the face. And n represents the normal unit vector of the face under consideration.

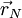If \vec r_{P} and \vec r_{N} are position vector of centroids of cells P and N respectively. Then, we define
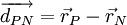
\overrightarrow{d_{PN}}= \vec r_{P} - \vec r_{N}


We wish to approaximate the diffusive flux 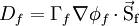D_f = \Gamma _f \nabla \phi _f \cdot{\rm{\vec S_f}} at the face.


Approach 1

A first approach is to use a simple expression for estimating the gradient of a scalar normal to the face.

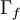D_f = \Gamma _f \nabla \phi _f \cdot \vec S_f = \Gamma _f \left[ {\left( {\phi _N - \phi _P } \right)\left| {{{\vec S_f} \over {\overrightarrow{d_{PN}}}}} \right|} \right]

where \Gamma _f is a suitable face average.

This approach is not very good when the non-orthogonality of the faces increases. If this is the case, it is advisable to use one of the following approaches.


Approach 2

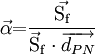
We define the vector \vec \alpha {\rm{ = }}\frac{{{\rm{\vec {S_f}}}}}{{{\rm{\vec S_f}} \cdot {\overrightarrow{d_{PN}}}}}

giving us the expression:

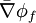D_f = \Gamma _f \nabla \phi _f \cdot{\rm{\vec S_f = }}\Gamma _{\rm{f}} \left[ {\left( {\phi _N - \phi _P } \right)\vec \alpha \cdot {\rm{\vec S_f + }}\bar \nabla \phi_f \cdot {\rm{\vec S_f - }}\left( {\bar \nabla \phi_f \cdot {\overrightarrow{d_{PN}}}} \right)\vec \alpha \cdot {\rm{\vec S_f}}} \right]

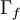where \bar \nabla \phi _f and \Gamma _f are suitable face averages.

References

  1. Ferziger, J.H. and Peric, M. (2001), Computational Methods for Fluid Dynamics, ISBN 3540420746, 3rd Rev. Ed., Springer-Verlag, Berlin..
  2. Hrvoje, Jasak (1996), "Error Analysis and Estimation for the Finite Volume Method with Applications to Fluid Flows", PhD Thesis, Imperial College, University of London (download).


Return to Numerical Methods

Retrieved from "https://openfoam.cfd-online.com/Wiki/Diffusion_term"
My wiki