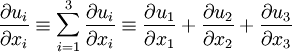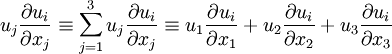Einstein summation convention
From CFD-Wiki
(Difference between revisions)
| Line 1: | Line 1: | ||
The Einstein summation convention is a tensor notation which is commonly used to implicitly define a sum. The convention states that as soon as one index is repeated in a term that implies a sum over all possible values for that index. | The Einstein summation convention is a tensor notation which is commonly used to implicitly define a sum. The convention states that as soon as one index is repeated in a term that implies a sum over all possible values for that index. | ||
| - | Here | + | Here are two examples: |
:<math> | :<math> | ||
\frac{\partial u_i}{\partial x_i} \equiv \sum_{i=1}^3 \frac{\partial u_i}{\partial x_i} \equiv \frac{\partial u_1}{\partial x_1} + \frac{\partial u_2}{\partial x_2} + \frac{\partial u_3}{\partial x_3} | \frac{\partial u_i}{\partial x_i} \equiv \sum_{i=1}^3 \frac{\partial u_i}{\partial x_i} \equiv \frac{\partial u_1}{\partial x_1} + \frac{\partial u_2}{\partial x_2} + \frac{\partial u_3}{\partial x_3} | ||
| + | </math> | ||
| + | |||
| + | :<math> | ||
| + | u_j\frac{\partial u_i}{\partial x_j} \equiv \sum_{j=1}^3 u_j\frac{\partial u_i}{\partial x_j} \equiv u_1\frac{\partial u_i}{\partial x_1} + u_2\frac{\partial u_i}{\partial x_2} + u_3\frac{\partial u_i}{\partial x_3} | ||
</math> | </math> | ||
Revision as of 10:04, 28 November 2005
The Einstein summation convention is a tensor notation which is commonly used to implicitly define a sum. The convention states that as soon as one index is repeated in a term that implies a sum over all possible values for that index.
Here are two examples: