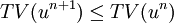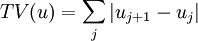TVD scheme
From CFD-Wiki
(Difference between revisions)
| (2 intermediate revisions not shown) | |||
| Line 3: | Line 3: | ||
:<math> | :<math> | ||
TV(u^{n+1}) \le TV(u^n) | TV(u^{n+1}) \le TV(u^n) | ||
| + | </math> | ||
| + | |||
| + | The total variation of a grid function is defined as | ||
| + | |||
| + | :<math> | ||
| + | TV(u) = \sum_j | u_{j+1} - u_j| | ||
</math> | </math> | ||
Note that a TVD scheme may not satisfy the entropy condition and hence can give incorrect solution. We have the following relationship between monotone, TVD and monotonicity preserving schemes, | Note that a TVD scheme may not satisfy the entropy condition and hence can give incorrect solution. We have the following relationship between monotone, TVD and monotonicity preserving schemes, | ||
| - | + | : [[Monotone scheme]] <math>\Longrightarrow</math> [[TVD scheme]] <math>\Longrightarrow</math> [[Monotonicity preserving scheme]] | |
==TVD condition: Incremental form== | ==TVD condition: Incremental form== | ||
==TVD condition: Viscosity form== | ==TVD condition: Viscosity form== | ||
| + | |||
| + | {{Stub}} | ||
Latest revision as of 21:28, 15 October 2005
A scheme is said to be TVD or Total Variation Diminishing if it does not increase the total variation of the solution, i.e.,
The total variation of a grid function is defined as
Note that a TVD scheme may not satisfy the entropy condition and hence can give incorrect solution. We have the following relationship between monotone, TVD and monotonicity preserving schemes,
- Monotone scheme
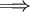TVD scheme 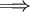Monotonicity preserving scheme
