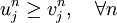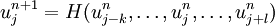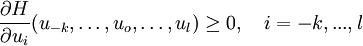Monotone scheme
From CFD-Wiki
(Difference between revisions)
| Line 18: | Line 18: | ||
\frac{\partial H}{\partial u_i}(u_{-k}, \dots, u_{o}, \ldots, u_{l}) \ge 0, \quad i=-k,...,l | \frac{\partial H}{\partial u_i}(u_{-k}, \dots, u_{o}, \ldots, u_{l}) \ge 0, \quad i=-k,...,l | ||
</math> | </math> | ||
| + | |||
| + | We have the following relationship between monotone, TVD and monotonicity preserving schemes, | ||
| + | |||
| + | [[Monotone scheme]] <math>\Longrightarrow</math> [[TVD scheme]] <math>\Longrightarrow</math> [[Monotonicity preserving scheme]] | ||
Revision as of 04:02, 30 September 2005
A scheme is said to be monotone if for two initial conditions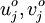 
with 
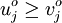, then
A monotone scheme for a scalar conservation law can be shown to converge to the unique entropy satisfying solution. However, monotone schemes can be at most first order accurate.
If the scheme can be written as
then it is monotone if and only if it is an increasing function of all its arguments. If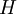 
is a differentiable function of its arguments, then the scheme is monotone if
We have the following relationship between monotone, TVD and monotonicity preserving schemes,
Monotone schemeTVD scheme
