Wall-adapting local eddy-viscosity (WALE) model
From CFD-Wiki
(Difference between revisions)
m |
|||
| (2 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
| + | In the WALE model the eddy viscosity is modeled by: <br> | ||
| + | |||
| + | |||
<math> \mu_{t} = \rho \Delta _s^2 \frac{(S_{ij}^{d} S_{ij}^{d})^{3/2}}{(\overline{S}_{ij} \overline{S}_{ij})^{5/2} + (S_{ij}^{d} S_{ij}^{d})^{5/4}} </math> | <math> \mu_{t} = \rho \Delta _s^2 \frac{(S_{ij}^{d} S_{ij}^{d})^{3/2}}{(\overline{S}_{ij} \overline{S}_{ij})^{5/2} + (S_{ij}^{d} S_{ij}^{d})^{5/4}} </math> | ||
| Line 7: | Line 10: | ||
<math> \overline{g}_{ij} = \frac{\partial \overline{u_i}}{\partial x_{j}} </math> | <math> \overline{g}_{ij} = \frac{\partial \overline{u_i}}{\partial x_{j}} </math> | ||
| + | |||
| + | <math> \overline{g}_{ij}^{2} = \overline{g}_{ik} \overline{g}_{kj} </math> | ||
where <math> | where <math> | ||
Latest revision as of 08:31, 19 May 2018
In the WALE model the eddy viscosity is modeled by:
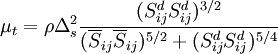
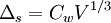
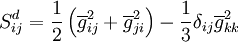
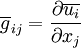

where 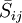 is the rate-of-strain tensor for the resolved scale defined by
is the rate-of-strain tensor for the resolved scale defined by
Where the constant 

