Arbitrary polyhedral volume
From CFD-Wiki
(Difference between revisions)
m |
|||
| Line 1: | Line 1: | ||
== Arbitrary Polyhedral Volume == | == Arbitrary Polyhedral Volume == | ||
| - | + | ||
| - | The volume of arbitrary polyhedral can be calculated by using Green-Gauss Theorem. | + | The volume of arbitrary polyhedral can be calculated by using [[Greens theorem | Green-Gauss Theorem]]. |
| - | <math>\int\limits_\Omega {div(\vec F)d\Omega = } \oint\limits_S {\vec F \bullet d\vec S} | + | |
| + | :<math>\int\limits_\Omega {div(\vec F)d\Omega = } \oint\limits_S {\vec F \bullet d\vec S} | ||
</math> | </math> | ||
| - | + | ||
| - | By choosing the function | + | By choosing the function |
| - | <math> | + | |
| + | :<math> | ||
\vec F = \frac{{\left( {x\hat i + y\hat j + z\hat k} \right)}}{3} | \vec F = \frac{{\left( {x\hat i + y\hat j + z\hat k} \right)}}{3} | ||
| - | </math> | + | </math> |
| + | |||
Where (x,y,z) are centroid of the surface enclosing the volume under consideration. | Where (x,y,z) are centroid of the surface enclosing the volume under consideration. | ||
| - | As we have, | + | As we have, |
| - | <math> | + | |
| + | :<math> | ||
div(\vec F) = 1 | div(\vec F) = 1 | ||
| - | </math | + | </math> |
| - | Hence the volume can be calculated as: | + | |
| - | <math> | + | Hence the volume can be calculated as: |
| + | |||
| + | :<math> | ||
volume = \oint\limits_S {\vec F \bullet \hat ndS} | volume = \oint\limits_S {\vec F \bullet \hat ndS} | ||
| - | </math | + | </math> |
| - | where the normal of the surface pointing outwards is given by: | + | |
| - | <math> | + | where the normal of the surface pointing outwards is given by: |
| + | |||
| + | :<math> | ||
\hat n = (n_x \hat i + n_y \hat j + n_z \hat k) | \hat n = (n_x \hat i + n_y \hat j + n_z \hat k) | ||
| - | </math> | + | </math> |
| + | |||
Final expression could be written as <br> | Final expression could be written as <br> | ||
| - | <math> | + | |
| + | :<math> | ||
volume = \frac{1}{3}\sum\limits_{faces} {\left[ {\left( {x \times n_x + y \times n_y + z \times n_z } \right) \bullet S} \right]} | volume = \frac{1}{3}\sum\limits_{faces} {\left[ {\left( {x \times n_x + y \times n_y + z \times n_z } \right) \bullet S} \right]} | ||
| - | </math> | + | </math> |
| + | |||
where S is magnitude of Surface Area. | where S is magnitude of Surface Area. | ||
| - | |||
Revision as of 14:03, 12 September 2005
Arbitrary Polyhedral Volume
The volume of arbitrary polyhedral can be calculated by using Green-Gauss Theorem.
By choosing the function
Where (x,y,z) are centroid of the surface enclosing the volume under consideration. As we have,
Hence the volume can be calculated as:
where the normal of the surface pointing outwards is given by:
Final expression could be written as
where S is magnitude of Surface Area.

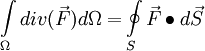

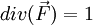
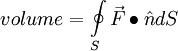
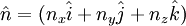
![volume = \frac{1}{3}\sum\limits_{faces} {\left[ {\left( {x \times n_x + y \times n_y + z \times n_z } \right) \bullet S} \right]}](/W/images/math/7/5/0/750f770a268adfcfe7d6f4019a66fe61.png)