Greens theorem
From CFD-Wiki
(Difference between revisions)
m (Greens Theorem moved to Greens theorem) |
m |
||
| Line 1: | Line 1: | ||
''Greens Theorem'', also known as ''Divergence Theorem'' is an important identity in vector calculus. If <math>u_i</math> is a vector field variable defined over a domain <math>\Omega</math> then Greens Theorem states that | ''Greens Theorem'', also known as ''Divergence Theorem'' is an important identity in vector calculus. If <math>u_i</math> is a vector field variable defined over a domain <math>\Omega</math> then Greens Theorem states that | ||
| - | <math> | + | :<math> |
\int_\Omega \frac{\partial u_i}{\partial x_i} dV = \oint_{\partial \Omega} u_i n_i dS | \int_\Omega \frac{\partial u_i}{\partial x_i} dV = \oint_{\partial \Omega} u_i n_i dS | ||
</math> | </math> | ||
where <math>\partial\Omega</math> represents the boundary of <math>\Omega</math> and <math>n_i</math> is the unit outward normal to <math>\partial\Omega</math>. | where <math>\partial\Omega</math> represents the boundary of <math>\Omega</math> and <math>n_i</math> is the unit outward normal to <math>\partial\Omega</math>. | ||
Latest revision as of 11:40, 12 September 2005
Greens Theorem, also known as Divergence Theorem is an important identity in vector calculus. If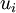 
is a vector field variable defined over a domain 
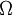then Greens Theorem states that
where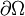 
represents the boundary of 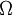and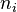 
is the unit outward normal to .
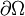