CFD Online Logo CFD Online URL
www.cfd-online.com
[Sponsors]
Home > Wiki > Favre averaged Navier-Stokes equations

Favre averaged Navier-Stokes equations

From CFD-Wiki

(Difference between revisions)
Jump to: navigation, search
Line 6: Line 6:
\frac{\partial \rho}{\partial t} +
\frac{\partial \rho}{\partial t} +
\frac{\partial}{\partial x_j}\left[ \rho u_j \right] = 0
\frac{\partial}{\partial x_j}\left[ \rho u_j \right] = 0
-
</math>
+
</math> (1)
-
</span>
+
-
<math>
+
:<math>
\frac{\partial}{\partial t}\left( \rho u_i \right) +
\frac{\partial}{\partial t}\left( \rho u_i \right) +
\frac{\partial}{\partial x_j}
\frac{\partial}{\partial x_j}
\left[ \rho u_i u_j + p \delta_{ij} - \tau_{ji} \right] = 0
\left[ \rho u_i u_j + p \delta_{ij} - \tau_{ji} \right] = 0
-
</math>
+
</math> (2)
-
<math>
+
:<math>
\frac{\partial}{\partial t}\left( \rho e_0 \right) +
\frac{\partial}{\partial t}\left( \rho e_0 \right) +
\frac{\partial}{\partial x_j}
\frac{\partial}{\partial x_j}
\left[ \rho u_j e_0 + u_j p + q_j - u_i \tau_{ij} \right] = 0
\left[ \rho u_j e_0 + u_j p + q_j - u_i \tau_{ij} \right] = 0
-
</math>
+
</math> (3)
For a Newtonian fluid, assuming Stokes Law for mono-atomic gases, the viscous
For a Newtonian fluid, assuming Stokes Law for mono-atomic gases, the viscous

Revision as of 08:09, 5 September 2005

The instantaneous continuity equation, momentum equation and energy equation for a compressible fluid can be written as:

\frac{\partial \rho}{\partial t} + \frac{\partial}{\partial x_j}\left[ \rho u_j \right] = 0 (1)
\frac{\partial}{\partial t}\left( \rho u_i \right) + \frac{\partial}{\partial x_j} \left[ \rho u_i u_j + p \delta_{ij} - \tau_{ji} \right] = 0 (2)
\frac{\partial}{\partial t}\left( \rho e_0 \right) + \frac{\partial}{\partial x_j} \left[ \rho u_j e_0 + u_j p + q_j - u_i \tau_{ij} \right] = 0 (3)

For a Newtonian fluid, assuming Stokes Law for mono-atomic gases, the viscous stress is given by:

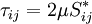
\tau_{ij} = 2 \mu S_{ij}^*

Where the trace-less viscous strain-rate is defined by:

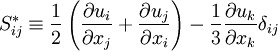
S_{ij}^* \equiv \frac{1}{2} \left(\frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i} \right) - \frac{1}{3} \frac{\partial u_k}{\partial x_k} \delta_{ij}

The heat-flux, 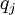q_j, is given by Fourier's law:

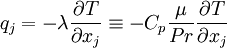
q_j = -\lambda \frac{\partial T}{\partial x_j} \equiv -C_p \frac{\mu}{Pr} \frac{\partial T}{\partial x_j}

Where the laminar Prandtl number Pr is defined by:

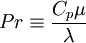
Pr \equiv \frac{C_p \mu}{\lambda}

To close these equations it is also necessary to specify an equation of state. Assuming a calorically perfect gas the following relations are valid:

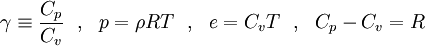
\gamma \equiv \frac{C_p}{C_v} ~~,~~ p = \rho R T ~~,~~ e = C_v T ~~,~~ C_p - C_v = R

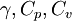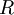Where \gamma, C_p, C_v and R are constant.

The total energy 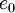e_0 is defined by:

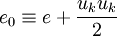
e_0 \equiv e + \frac{u_k u_k}{2}

Note that the corresponding expression~\ref{eq:fav_total_energy} for Favre averaged turbulent flows contains an extra term related to the turbulent energy.



\frac{\partial \overline{\rho}}{\partial t} + \frac{\partial}{\partial x_i}\left[ \overline{\rho} \widetilde{u_i} \right] = 0

\frac{\partial}{\partial t}\left( \overline{\rho} \widetilde{u_i} \right) + \frac{\partial}{\partial x_j} \left[ \overline{\rho} \widetilde{u_j} \widetilde{u_i} + \overline{p} \delta_{ij} - \widetilde{\tau_{ji}^{tot}} \right] = 0

#total_energy

Retrieved from "https://openfoam.cfd-online.com/Wiki/Favre_averaged_Navier-Stokes_equations"
My wiki