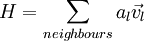CFD Online Logo CFD Online URL
www.cfd-online.com
[Sponsors]
Home > Wiki > Rhie-Chow interpolation

Rhie-Chow interpolation

From CFD-Wiki

(Difference between revisions)
Jump to: navigation, search
 
(7 intermediate revisions not shown)
Line 1: Line 1:
we have at each cell descretised equation in this form, <br>
we have at each cell descretised equation in this form, <br>
:<math> a_p \vec v_P  = \sum\limits_{neighbours} {a_l } \vec v_l  - \frac{{\nabla p}}{V} </math> ;  <br>
:<math> a_p \vec v_P  = \sum\limits_{neighbours} {a_l } \vec v_l  - \frac{{\nabla p}}{V} </math> ;  <br>
-
we have <br>
+
For continuity we have <br>
-
:<math> \vec v_P  = \frac{{\sum\limits_{neighbours} {a_l } \vec v_l }}{{a_p }} - \frac{{\nabla p}}{{a_p V}} </math> <br>
+
:<math> \sum\limits_{faces} \left[ {\frac{1}{{a_p }}H} \right]_{face}  = \sum\limits_{faces} \left[ {\frac{1}{{a_p }}\frac{{\nabla p}}{V}} \right]_{face} </math> <br>
-
For continuity : <br>
+
where <br>
-
:<math> \sum\limits_{faces} {\vec v_f  \bullet \vec A}  = 0 </math> <br>
+
:<math> H = \sum\limits_{neighbours} {a_l } \vec v_l </math> <br>
-
so we get: <br>
+
-
:<math>\left[ {\frac{{\sum\limits_{neighbours} {a_l } \vec v_l }}{{a_p }}} \right]_{face}  - \left[ {\frac{{\nabla p}}{{a_p V}}} \right]_{face}  = 0 </math> <br>
+
-
this gives us: <br>
+
-
:<math> \left[ {\frac{{\sum\limits_{neighbours} {a_l } \vec v_l }}{{a_p }}} \right]_{face}  = \left[ {\frac{{\nabla p}}{{a_p V}}} \right]_{face} </math><br>
+
-
defining <math> H = \sum\limits_{neighbours} {a_l } \vec v_l </math> <br>
+
-
:<math> \left[ {\frac{1}{{a_p }}H} \right]_{face}  = \left[ {\frac{1}{{a_p }}\frac{{\nabla p}}{V}} \right]_{face} </math> <br>
+
-
from this a pressure correction equation could be formed as: <br>
+
-
:<math> \left[ {\frac{1}{{a_p }}H} \right]_{face}  - \left[ {\frac{1}{{a_p }}\frac{{\nabla p^* }}{V}} \right]_{face}  = \left[ {\frac{1}{{a_p }}\frac{{\nabla p^' }}{V}} \right]_{face}  </math> <br>
+
-
This is a poisson equation.
+
-
Here the gradients could be used from previous iteration.
+
This interpolation of variables H and <math> {\nabla p} </math> based on coefficients <math> a_p </math> for [[Velocity-pressure coupling | pressure velocity coupling  ]] is called <b>Rhie-Chow interpolation</b>.
 +
 
 +
the Rhie-Chow interpolation is the same as adding a pressure term, which is proportional to a third derivative of the pressue
 +
 
 +
----
 +
<i> Return to: <br>
 +
# [[Numerical methods | Numerical Methods]]
 +
# [[Solution of Navier-Stokes equation]]
 +
</i>

Latest revision as of 06:14, 27 August 2012

we have at each cell descretised equation in this form,

a_p \vec v_P = \sum\limits_{neighbours} {a_l } \vec v_l - \frac{{\nabla p}}{V}  ;

For continuity we have

\sum\limits_{faces} \left[ {\frac{1}{{a_p }}H} \right]_{face} = \sum\limits_{faces} \left[ {\frac{1}{{a_p }}\frac{{\nabla p}}{V}} \right]_{face}

where

H = \sum\limits_{neighbours} {a_l } \vec v_l

This interpolation of variables H and 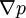{\nabla p} based on coefficients 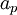a_p for pressure velocity coupling is called Rhie-Chow interpolation.

the Rhie-Chow interpolation is the same as adding a pressure term, which is proportional to a third derivative of the pressue

Return to:

  1. Numerical Methods
  2. Solution of Navier-Stokes equation

Retrieved from "https://openfoam.cfd-online.com/Wiki/Rhie-Chow_interpolation"
My wiki