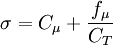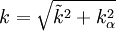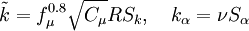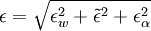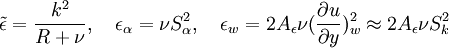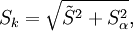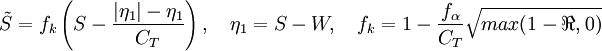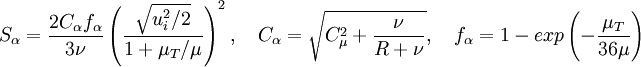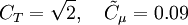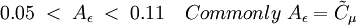Rahman-Siikonen-Agarwal Model
From CFD-Wiki
(Difference between revisions)
(Created page with "== Introduction == The Rahman-Agarwal-Siikonen (RAS) Turbulence model is a one-equation eddy viscosity model based on <math>k-\epsilon</math> closure. The R-transport equation ...") |
(→RAS Model) |
||
| Line 5: | Line 5: | ||
== RAS Model == | == RAS Model == | ||
| - | The turbulent eddy viscosity is given by | + | '''The turbulent eddy viscosity is given by''' |
| + | |||
:<math> | :<math> | ||
| Line 11: | Line 12: | ||
</math> | </math> | ||
| - | The R-transport | + | |
| + | '''The R-transport Equation:''' | ||
:<math> | :<math> | ||
\begin{matrix} | \begin{matrix} | ||
| - | \frac{\partial \rho R}{\partial t} + \frac{\partial \rho u_j R}{\partial x_j} | + | \frac{\partial \rho R}{\partial t} + \frac{\partial \rho u_j R}{\partial x_j} = \frac{\partial}{\partial x_j} \biggl[ \left(\mu +\frac{\mu_t}{\sigma}\right)\frac{\partial R}{\partial x_j} \biggr] +C_1 \rho \sqrt{P \tilde{R}} - C_2 \rho \left(\frac{\partial \tilde{R}}{\partial x_k}\right)^2 |
\end{matrix} | \end{matrix} | ||
| + | </math> | ||
| + | |||
| + | |||
| + | '''Realizable Time Scale:''' | ||
| + | |||
| + | :<math> | ||
| + | T_t = \frac{k}{\epsilon} \sqrt{1+\frac{C_t^2}{Re_T}}, \quad Re_T = \frac{k^2}{\nu \epsilon} | ||
| + | </math> | ||
| + | |||
| + | |||
| + | '''Coefficient <math>C_\mu</math>:''' | ||
| + | |||
| + | :<math> | ||
| + | C_\mu = \frac{3(1+\eta^2)\alpha_1}{3+\eta^2+6\eta^2\xi^2+6\xi^2} | ||
| + | </math> | ||
| + | |||
| + | :<math> | ||
| + | \eta = \alpha_2 T_t S, \quad \xi = \alpha_3 T_t W | ||
| + | </math> | ||
| + | |||
| + | :<math> | ||
| + | \alpha_1 = g\left(\frac{1}{4}+\frac{2}{3}\Pi_b^{1/2}\right), \quad \alpha_2 = \frac{3}{8\sqrt{2}}g | ||
| + | </math> | ||
| + | |||
| + | :<math> | ||
| + | \alpha_3 = \frac{3}{\sqrt{2}}\alpha_2, \quad g = \left( 1+2\frac{P}{\epsilon} \right) ^{-1} | ||
| + | </math> | ||
| + | |||
| + | :<math> | ||
| + | \Pi_b = C_\nu \frac{P}{\epsilon}, \quad \frac{P}{\epsilon} = C_\nu \zeta^2 | ||
| + | </math> | ||
| + | |||
| + | :<math> | ||
| + | C_\nu = \frac{1}{2(1+T_t S \sqrt{1+\Re^2})}, \quad \zeta = T_t S max(1,\Re) | ||
| + | </math> | ||
| + | |||
| + | :<math> | ||
| + | S_{ij} = \frac{1}{2}\left(\frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i}\right), \quad S = \sqrt{2S_{ij} S_{ij}} | ||
| + | </math> | ||
| + | |||
| + | :<math> | ||
| + | W_{ij} = \frac{1}{2}\left(\frac{\partial u_i}{\partial x_j} - \frac{\partial u_j}{\partial x_i}\right), \quad W = \sqrt{2S_{ij} S_{ij}} | ||
| + | </math> | ||
| + | |||
| + | |||
| + | '''Damping Function:''' | ||
| + | |||
| + | :<math> | ||
| + | -L^2 \nabla^2f_\mu + f_\mu = 1 | ||
| + | </math> | ||
| + | |||
| + | :<math> | ||
| + | L^2 = \zeta(2\zeta+C_\mu Re_T)\sqrt{\frac{\nu^3}{\epsilon}}, \quad (f_\mu)_{wall} = 0 | ||
| + | </math> | ||
| + | |||
| + | |||
| + | '''Other Model Coefficients:''' | ||
| + | |||
| + | :<math> | ||
| + | C_1 = 2C_\mu \zeta (1-C_\mu \zeta), \quad C_2 = min \Biggl[ 2C_\mu,\; \tilde{C}_\mu \sqrt{1+\left( \frac{C_1}{6 \tilde{C}_\mu}\right)^2}\;\Biggr] | ||
| + | </math> | ||
| + | |||
| + | :<math> | ||
| + | \sigma = C_\mu + \frac{f_\mu}{C_T} | ||
| + | </math> | ||
| + | |||
| + | |||
| + | '''<math>k</math> and <math>\epsilon</math>:''' | ||
| + | |||
| + | :<math> | ||
| + | k = \sqrt{\tilde{k}^2 + k_\alpha ^2} | ||
| + | </math> | ||
| + | |||
| + | :<math> | ||
| + | \tilde{k} = f_\mu^{0.8}\sqrt{C_\mu}R S_k, \quad k_\alpha = \nu S_\alpha | ||
| + | </math> | ||
| + | |||
| + | |||
| + | :<math> | ||
| + | \epsilon = \sqrt{\epsilon_w^2+\tilde{\epsilon}^2+\epsilon_\alpha^2} | ||
| + | </math> | ||
| + | |||
| + | :<math> | ||
| + | \tilde{\epsilon} = \frac{k^2}{R+\nu}, \quad \epsilon_\alpha = \nu S_\alpha^2, \quad \epsilon_w=2A_\epsilon\nu(\frac{\partial u}{\partial y})_w^2\approx 2A_\epsilon \nu S_k^2 | ||
| + | </math> | ||
| + | |||
| + | |||
| + | :<math> | ||
| + | S_k = \sqrt{\tilde{S}^2+S_\alpha^2}, | ||
| + | </math> | ||
| + | |||
| + | :<math> | ||
| + | \tilde{S} = f_k\left(S-\frac{\vert\eta_1\vert - \eta_1}{C_T}\right), \quad \eta_1 = S-W, \quad f_k=1-\frac{f_\alpha}{C_T}\sqrt{max(1-\Re,0)} | ||
| + | </math> | ||
| + | |||
| + | :<math> | ||
| + | S_\alpha = \frac{2C_\alpha f_\alpha}{3\nu}\left(\frac{\sqrt{u_i^2/2}}{1+\mu_T/\mu}\right)^2, \quad C_\alpha=\sqrt{C_\mu^2+\frac{\nu}{R+\nu}}, \quad f_\alpha = 1 - exp\left(-\frac{\mu_T}{36\mu}\right) | ||
| + | </math> | ||
| + | |||
| + | '''Constants:''' | ||
| + | |||
| + | :<math> | ||
| + | C_T = \sqrt{2}, \quad \tilde{C}_\mu = 0.09 | ||
| + | </math> | ||
| + | |||
| + | :<math> | ||
| + | 0.05\;<\;A_\epsilon\;<\;0.11 \quad Commonly \;A_\epsilon = \tilde{C}_\mu | ||
</math> | </math> | ||
Revision as of 22:01, 14 August 2012
Introduction
The Rahman-Agarwal-Siikonen (RAS) Turbulence model is a one-equation eddy viscosity model based on 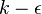 closure. The R-transport equation along with the Bradshaw and other empirical relations are used to solve for the turbulent viscosity. A damping function,
closure. The R-transport equation along with the Bradshaw and other empirical relations are used to solve for the turbulent viscosity. A damping function, 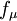 , is used to represent the kinematic blocking by the wall. To avoid defining a wall distance, a Helmholtz-type elliptic relaxation equation is used for
, is used to represent the kinematic blocking by the wall. To avoid defining a wall distance, a Helmholtz-type elliptic relaxation equation is used for 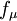 . The model has been validated against a few well-documented flow cases, yielding predictions in good agreement with DNS and experimental data.
. The model has been validated against a few well-documented flow cases, yielding predictions in good agreement with DNS and experimental data.
RAS Model
The turbulent eddy viscosity is given by
The R-transport Equation:
Realizable Time Scale:
Coefficient 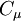 :
:
Damping Function:
Other Model Coefficients:
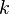 and
and  :
:
Constants:

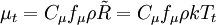
![\begin{matrix}
\frac{\partial \rho R}{\partial t} + \frac{\partial \rho u_j R}{\partial x_j} = \frac{\partial}{\partial x_j} \biggl[ \left(\mu +\frac{\mu_t}{\sigma}\right)\frac{\partial R}{\partial x_j} \biggr] +C_1 \rho \sqrt{P \tilde{R}} - C_2 \rho \left(\frac{\partial \tilde{R}}{\partial x_k}\right)^2
\end{matrix}](/W/images/math/d/3/2/d3291f6d4f59689da557c0eef4170cd4.png)

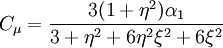

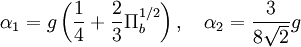
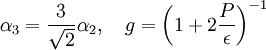
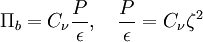
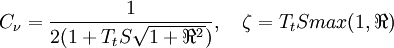
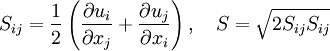
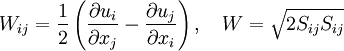
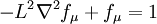

![C_1 = 2C_\mu \zeta (1-C_\mu \zeta), \quad C_2 = min \Biggl[ 2C_\mu,\; \tilde{C}_\mu \sqrt{1+\left( \frac{C_1}{6 \tilde{C}_\mu}\right)^2}\;\Biggr]](/W/images/math/4/a/7/4a7662c3bf356b3a87d6eb5a62cd91a7.png)