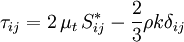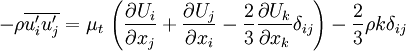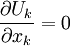Boussinesq eddy viscosity assumption
From CFD-Wiki
(Difference between revisions)
m (Reverted edits by Simonatkins (Talk) to last version by Peter) |
|||
| (6 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
| - | In 1877 Boussinesq postulated that the momentum transfer caused by turbulent eddies can be modeled with an eddy viscosity. This is in analogy with how the momentum transfer caused by the molecular motion in a gas can be described by a molecular viscosity. The Boussinesq assumption states that the [[Reynolds stress tensor]], <math>\tau_{ij}</math>, is proportional to the trace-less mean strain rate tensor, <math>S_{ij}^*</math>, and can be written in the following way: | + | In 1877 Boussinesq postulated<ref>{{Citation |
| + | | last =Boussinesq | first = J. | ||
| + | | journal = Mémoires présentés par divers savants à l'Académie des Sciences | ||
| + | | number = 1 | ||
| + | | pages = 1-680 | ||
| + | | title = Essai sur la théorie des eaux courantes | ||
| + | | volume = 23 | ||
| + | | address = Paris | ||
| + | | year = 19877 | ||
| + | }}</ref><ref> | ||
| + | {{Citation | ||
| + | | last =Schmitt | first = F.G. | ||
| + | | journal = Comptes Rendus Mécanique | ||
| + | | number = (9-10) | ||
| + | | pages = 617-627 | ||
| + | | title = About Boussinesq’s turbulent viscosity hypothesis: historical remarks and a direct evaluation of its validity | ||
| + | | volume = 335 | ||
| + | | url = http://hal.archives-ouvertes.fr/hal-00264386/fr/ | ||
| + | | year = 2007 | ||
| + | }} | ||
| + | </ref> that the momentum transfer caused by turbulent eddies can be modeled with an eddy viscosity. This is in analogy with how the momentum transfer caused by the molecular motion in a gas can be described by a molecular viscosity. The Boussinesq assumption states that the [[Reynolds stress tensor]], <math>\tau_{ij}</math>, is proportional to the trace-less mean strain rate tensor, <math>S_{ij}^*</math>, and can be written in the following way: | ||
:<math>\tau_{ij} = 2 \, \mu_t \, S_{ij}^* - \frac{2}{3} \rho k \delta_{ij}</math> | :<math>\tau_{ij} = 2 \, \mu_t \, S_{ij}^* - \frac{2}{3} \rho k \delta_{ij}</math> | ||
| Line 12: | Line 32: | ||
The Boussinesq eddy viscosity assumption is also often called the Boussinesq hypothesis or the Boussinesq approximation. | The Boussinesq eddy viscosity assumption is also often called the Boussinesq hypothesis or the Boussinesq approximation. | ||
| - | + | == See also == | |
| + | *[[Two equation models]] | ||
| + | *[[Introduction to turbulence/Reynolds averaged equations#Turbulence closure problem and eddy viscosity|Turbulence closure problem and eddy viscosity]] | ||
==References== | ==References== | ||
| - | + | {{reflist}} | |
| - | {{ | + | |
| - | + | ||
| - | + | ||
{{stub}} | {{stub}} | ||
Latest revision as of 09:15, 3 January 2012
In 1877 Boussinesq postulated[1][2] that the momentum transfer caused by turbulent eddies can be modeled with an eddy viscosity. This is in analogy with how the momentum transfer caused by the molecular motion in a gas can be described by a molecular viscosity. The Boussinesq assumption states that the Reynolds stress tensor,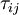 
, is proportional to the trace-less mean strain rate tensor, 
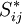, and can be written in the following way:
Where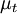 
is a scalar property called the eddy viscosity. The same equation can be written more explicitly as:
Note that for incompressible flow:
The Boussinesq eddy viscosity assumption is also often called the Boussinesq hypothesis or the Boussinesq approximation.
See also
References
- ↑ Boussinesq, J. (19877), "Essai sur la théorie des eaux courantes", Mémoires présentés par divers savants à l'Académie des Sciences 23 (1): 1-680
- ↑ Schmitt, F.G. (2007), "About Boussinesq’s turbulent viscosity hypothesis: historical remarks and a direct evaluation of its validity", Comptes Rendus Mécanique 335 ((9-10)): 617-627
