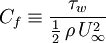CFD Online Logo CFD Online URL
www.cfd-online.com
[Sponsors]
Home > Wiki > Skin friction coefficient

Skin friction coefficient

From CFD-Wiki

(Difference between revisions)
Jump to: navigation, search
Line 5: Line 5:
Where <math>\tau_w</math> is the local [[wall shear stress]], <math>\rho</math> is the fluid density and <math>U_\infty</math> is the free-stream velocity (usually taken ouside of the boundary layer or at the inlet).
Where <math>\tau_w</math> is the local [[wall shear stress]], <math>\rho</math> is the fluid density and <math>U_\infty</math> is the free-stream velocity (usually taken ouside of the boundary layer or at the inlet).
 +
For a turbulent boundary layer several approximation formulas for the local skin friction can be used:
-
It is related to the momentum thickness as follows: C_f = 2(d theta)/ (d x)
+
1/7 power law:
-
An empirical relation you may use for comparison is: C_f = 0.0583/(Re )^0.2
+
<math>C_f = 0.0576 Re_x^{-1/5} \quad \mbox{for} \quad 5 \cdot 10^5 < Re_x < 10^7 </math>
 +
1/7 power law with experimental calibration (equation 21.12 in [1]):
-
''Someone should add some correlations and references for them here''
+
<math>C_f = 0.0592 \, Re_x^{-1/5} \quad \mbox{for} \quad 5 \cdot 10^5 < Re_x < 10^7</math> (equation 21.12 in [1])
 +
 
 +
Schlichting (equation 21.16 footnote in [1])
 +
 
 +
<math>C_f = [ 2 \, log(Re_x) - 0.65 ] ^{-2.3} \quad \mbox{for} \quad 5 \cdot Re_x < 10^9 </math>
 +
 
 +
Schultz-Grunov (equation 21.19a in [1]):
 +
 
 +
<math>C_f = 0.370 \, [ log(Re_x) ]^{-2.584} </math>
 +
 
 +
== References ==
 +
 
 +
# {{reference-book|author=Schlichting, Hermann |year=1979|title=Boundary Layer Theory|rest=ISBN 0-07-055334-3, 7th Edition}}
 +
 
 +
== To do ==
 +
 
 +
''Someone should add more data about total skin friction approximations, Prandtl-Schlichting skin-friction formula, and the Karman-Schoenherr equation.''
{{stub}}
{{stub}}

Revision as of 14:45, 25 February 2011

The skin friction coefficient, C_f, is defined by:

C_f \equiv \frac{\tau_w}{\frac{1}{2} \, \rho \, U_\infty^2}

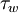Where \tau_w is the local wall shear stress, 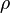\rho is the fluid density and U_\infty is the free-stream velocity (usually taken ouside of the boundary layer or at the inlet).

For a turbulent boundary layer several approximation formulas for the local skin friction can be used:

1/7 power law:

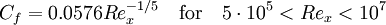
C_f = 0.0576 Re_x^{-1/5} \quad \mbox{for} \quad 5 \cdot 10^5 < Re_x < 10^7

1/7 power law with experimental calibration (equation 21.12 in [1]):

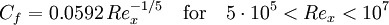C_f = 0.0592 \, Re_x^{-1/5} \quad \mbox{for} \quad 5 \cdot 10^5 < Re_x < 10^7 (equation 21.12 in [1])

Schlichting (equation 21.16 footnote in [1])

C_f = [ 2 \, log(Re_x) - 0.65 ] ^{-2.3} \quad \mbox{for} \quad 5 \cdot Re_x < 10^9

Schultz-Grunov (equation 21.19a in [1]):

C_f = 0.370 \, [ log(Re_x) ]^{-2.584}

References

  1. Schlichting, Hermann (1979), Boundary Layer Theory, ISBN 0-07-055334-3, 7th Edition.

To do

Someone should add more data about total skin friction approximations, Prandtl-Schlichting skin-friction formula, and the Karman-Schoenherr equation.


This article is a stub, a short article which needs to be improved. You can help by expanding it.
Retrieved from "https://openfoam.cfd-online.com/Wiki/Skin_friction_coefficient"
My wiki